
分析 (1)根据曲线y=f(x)与曲线y=g(x)在它们的交点(2,c)处具有公共切线,可知切点处的函数值相等,切点处的斜率相等,故可求a、b的值;
(2)①根据函数h(x)的单调递减区间为[-$\frac{a}{2}$,-$\frac{\sqrt{b}}{3}$]得出a2=4b,构建函数h(x)=f(x)+g(x)=x3+ax2+$\frac{1}{4}$a2x+1,求导函数,利用导数的正负,可确定函数的单调区间,进而分类讨论,确定函数在区间(-∞,-1)上的最大值.
②由①知,函数h(x)在(-∞,-$\frac{a}{2}$)单调递增,在(-$\frac{a}{2}$,-$\frac{a}{6}$)单调递减,在(-$\frac{a}{6}$,+∞)上单调递增,从而得出其极大值、极小值,再根据|h(x)|≤3,在x∈[-2,0]上恒成立,建立关于a的不等关系,解得a的取值范围即可.
解答 解:(1)f(x)=ax2+1(a>0),则f′(x)=2ax,k1=4a,g(x)=x3+bx,则f′(x)=3x2+b,k2=12+b,
由(2,c)为公共切点,可得:4a=12+b;
又f(2)=4a+1,g(2)=8+2b,
∴4a+1=8+2b,与4a=12+b联立可得:a=$\frac{17}{4}$,b=5;
(2)①由h(x)=f(x)+g(x)=x3+ax2+bx+1,
则h′(x)=3x2+2ax+b,
因函数h(x)的单调递减区间为[-$\frac{a}{2}$,-$\frac{\sqrt{b}}{3}$],∴当x∈[-$\frac{a}{2}$,-$\frac{\sqrt{b}}{3}$]时,3x2+2ax+b≤0恒成立,
此时,x=-$\frac{\sqrt{b}}{3}$是方程3x2+2ax+b=0的一个根,得3(-$\frac{\sqrt{b}}{3}$)2+2a(-$\frac{\sqrt{b}}{3}$)+b=0,得a2=4b,
∴h(x)=x3+ax2+$\frac{1}{4}$a2x+1;
令h′(x)=0,解得:x1=-$\frac{a}{2}$,x2=-$\frac{a}{6}$;
∵a>0,∴-$\frac{a}{2}$<-$\frac{a}{6}$,列表如下:
| x | (-∞,-$\frac{a}{2}$) | -$\frac{a}{2}$ | (-$\frac{a}{2}$,-$\frac{a}{6}$) | -$\frac{a}{6}$ | (-$\frac{a}{6}$,+∞) |
| h′(x) | + | - | + | ||
| h(x) | 极大值 | 极小值 |
点评 本题考查导数知识的运用,考查导数的几何意义,考查函数的单调性与最值,解题的关键是正确求出导函数和应用分类讨论的方法.


科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
| x | 24 | 15 | 23 | 19 | 16 | 11 | 20 | 16 | 17 | 13 |
| y | 92 | 79 | 97 | 89 | 64 | 47 | 83 | 68 | 71 | 59 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 1 | B. | 2 | C. | 3 | D. | 4 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
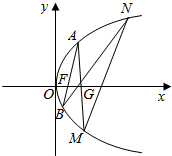 如图,已知抛物线C:y2=2px(p>0),焦点为F,过点G(p,0)作直线l交抛物线C于A,M两点,设A(x1,y1),M(x2,y2).
如图,已知抛物线C:y2=2px(p>0),焦点为F,过点G(p,0)作直线l交抛物线C于A,M两点,设A(x1,y1),M(x2,y2).查看答案和解析>>
科目:高中数学 来源: 题型:选择题
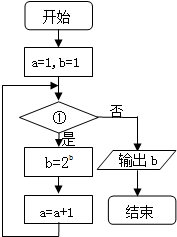 已知流程图如图所示,该程序运行后,为使输出的b值为16,则循环体的判断框内①处应填( )
已知流程图如图所示,该程序运行后,为使输出的b值为16,则循环体的判断框内①处应填( )| A. | a>3? | B. | a≥3? | C. | a≤3? | D. | a<3? |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com