
【题目】下列选项中说法正确的是( )
A.命题“p∨q为真”是命题“p∧q为真”的必要条件
B.向量 ![]() ,
, ![]() 满足
满足 ![]() ,则
,则 ![]() 与
与 ![]() 的夹角为锐角
的夹角为锐角
C.若am2≤bm2 , 则a≤b
D.“?x0∈R,x02﹣x0≤0”的否定是“?x∈R,x2﹣x≥0”
【答案】A
【解析】解:对于A,若p∨q为真命题,则p,q至少有一个为真命题,若p∧q为真命题,则p,q都为真命题,则“p∨q为真命题”是“p∧q为真命题”的必要不充分条件,正确; 对于B,根据向量数量积的定义,向量 ![]() ,
, ![]() 满足
满足 ![]() ,则
,则 ![]() 与
与 ![]() 的夹角为锐角或同向,故错;
的夹角为锐角或同向,故错;
对于C,如果m2=0时,am2≤bm2成立,a≤b不一定成立,故错;
对于D,“x0∈R,x02﹣x0≤0”的否定是“x∈R,x2﹣x>0”,故错.
故选:A.
【考点精析】根据题目的已知条件,利用命题的真假判断与应用的相关知识可以得到问题的答案,需要掌握两个命题互为逆否命题,它们有相同的真假性;两个命题为互逆命题或互否命题,它们的真假性没有关系.


 全能测控期末小状元系列答案
全能测控期末小状元系列答案科目:高中数学 来源: 题型:
【题目】在△ABC中,D为BC的中点,∠BAD+∠C≥90°. (Ⅰ)求证:sin2C≤sin2B;
(Ⅱ)若cos∠BAD=﹣ ![]() ,AB=2,AD=3,求AC.
,AB=2,AD=3,求AC.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,四棱锥P﹣ABCD中,PA⊥底面ABCD,底面ABCD是直角梯形,∠ADC=90°,AD∥BC,AB⊥AC,AB=AC= ![]() ,点E在AD上,且AE=2ED. (Ⅰ)已知点F在BC上,且CF=2FB,求证:平面PEF⊥平面PAC;
,点E在AD上,且AE=2ED. (Ⅰ)已知点F在BC上,且CF=2FB,求证:平面PEF⊥平面PAC;
(Ⅱ)当二面角A﹣PB﹣E的余弦值为多少时,直线PC与平面PAB所成的角为45°?
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在△ABC中,内角A、B、C的对边分别为a、b、c,且2asinB= ![]() b.
b.
(1)求角A的大小;
(2)若0<A< ![]() ,a=6,且△ABC的面积S=
,a=6,且△ABC的面积S= ![]() ,求△ABC的周长.
,求△ABC的周长.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】中国古代数学家赵爽设计的弦图(如图1)是由四个全等的直角三角形拼成,四个全等的直角三角形也可拼成图2所示的菱形,已知弦图中,大正方形的面积为100,小正方形的面积为4,则图2中菱形的一个锐角的正弦值为( ) 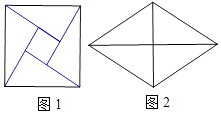
A.![]()
B.![]()
C.![]()
D.![]()
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com