
 如图,海上有A,B两个小岛相距10km,船O将保持观望A岛和B岛所成的视角为60°,现从船O上派下一只小艇沿BO方向驶至C处进行作业,且OC=BO.设AC=xkm.
如图,海上有A,B两个小岛相距10km,船O将保持观望A岛和B岛所成的视角为60°,现从船O上派下一只小艇沿BO方向驶至C处进行作业,且OC=BO.设AC=xkm.| 1 |
| 2 |
| ||
| 2x |
| 3 |
| 3 |
| 3 |
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
| 3 |
| 1 |
| 2 |
| ||
| 2 |
| 1 |
| 2 |
| ||
| 4 |
| 1 |
| 2 |
| 1 |
| 2 |
| ||
| 4 |
| ||
| 2x |
| ||
| 2x |
| 3 |
| ||
| 2 |
| 100 |
| x2 |
| 3 |
| 3 |
| ||||
2×10
|


 新非凡教辅冲刺100分系列答案
新非凡教辅冲刺100分系列答案科目:高中数学 来源: 题型:
查看答案和解析>>
科目:高中数学 来源:2013-2014学年四川成都外国语学校高三12月月考理科数学试卷(解析版) 题型:解答题
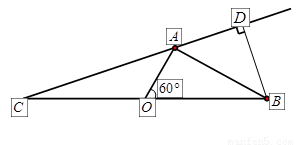
如图,海上有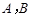 两个小岛相距10
两个小岛相距10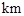 ,船O将保持观望A岛和B岛所成的视角为
,船O将保持观望A岛和B岛所成的视角为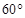 ,现从船O上派下一只小艇沿
,现从船O上派下一只小艇沿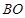 方向驶至
方向驶至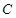 处进行作业,且
处进行作业,且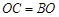 .设
.设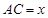
 。
。
(1)用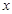 分别表示
分别表示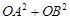 和
和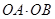 ,并求出
,并求出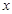 的取值范围;
的取值范围;
(2)晚上小艇在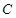 处发出一道强烈的光线照射A岛,B岛至光线
处发出一道强烈的光线照射A岛,B岛至光线 的距离为
的距离为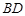 ,求BD的最大值.
,求BD的最大值.
查看答案和解析>>
科目:高中数学 来源:2013-2014学年四川成都外国语学校高三12月月考文科数学试卷(解析版) 题型:解答题
如图,海上有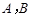 两个小岛相距10
两个小岛相距10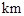 ,船O将保持观望A岛和B岛所成的视角为
,船O将保持观望A岛和B岛所成的视角为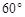 ,现从船O上派下一只小艇沿
,现从船O上派下一只小艇沿 方向驶至
方向驶至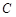 处进行作业,且
处进行作业,且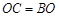 .设
.设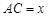
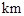 。
。
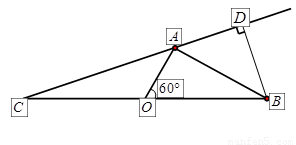
(1)用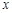 分别表示
分别表示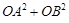 和
和 ,并求出
,并求出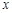 的取值范围;
的取值范围;
(2)晚上小艇在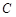 处发出一道强烈的光线照射A岛,B岛至光线
处发出一道强烈的光线照射A岛,B岛至光线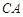 的距离为
的距离为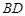 ,求BD的最大值.
,求BD的最大值.
查看答案和解析>>
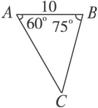
科目:高中数学 来源:2010年临川二中新余四中高三暑假联考文科数学卷 题型:填空题
如图:
海岸上有相距5海里的两座灯塔A、B,灯塔B位于灯塔A的正南方向,海上停泊着两艘轮船,甲船位于灯塔A的北偏西75°方向,与A相距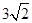 海里的D处;乙船位于灯塔B的北偏西60°方向,与B相距5海里的C处,则两艘轮船之间的距离为 海里.
海里的D处;乙船位于灯塔B的北偏西60°方向,与B相距5海里的C处,则两艘轮船之间的距离为 海里.

第16题图
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com