
【题目】2019年9月20日,黔东南州第十届旅游产业发展大会在凯里市举行,大会指出了交通对旅游业的发展有着深刻的影响,并引起了相关部门的高度重视.现针对凯里市区重要道路网中的![]() 个交通路段,依据其交通指数数据绘制的频率分布直方图如下图所示.(交通指数是综合反映道路网畅通或拥堵的概念性指数值,记为
个交通路段,依据其交通指数数据绘制的频率分布直方图如下图所示.(交通指数是综合反映道路网畅通或拥堵的概念性指数值,记为![]() ,其范围为
,其范围为![]() ,分别有五个级别:
,分别有五个级别:![]() ,畅通;
,畅通;![]() ,基本畅通;
,基本畅通;![]() ,轻度拥堵;
,轻度拥堵;![]() ,中度拥堵;
,中度拥堵;![]() ,严重拥堵)
,严重拥堵)
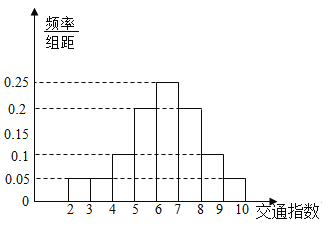
(1)利用频率分布直方图估计凯里市区这![]() 个交通路段的交通指数的众数与平均数.
个交通路段的交通指数的众数与平均数.
(2)用分层抽样的方法从轻度拥堵、中度拥堵、严重拥堵的路段中共抽取![]() 个路段,再从这
个路段,再从这![]() 个路段中任取
个路段中任取![]() 个,求至少有
个,求至少有![]() 个路段为中度拥堵的概率.
个路段为中度拥堵的概率.
【答案】(1)众数为![]() ,平均数6.3(2)
,平均数6.3(2)![]()
【解析】
(1)根据众数为频率分布直方图最高一组的组中值,平均数为各组的组中值与频率的乘积之和,计算可得;
(2)首先计算出各组抽取的数量,记抽取的![]() 个轻度拥堵路段为
个轻度拥堵路段为![]() ,
,![]() 个中度拥堵路段为
个中度拥堵路段为![]() ,
,![]() 个重度拥堵的路段为
个重度拥堵的路段为![]() ,用列举法将所有可能情况一一列举,再由古典概型的概率公式计算可得;
,用列举法将所有可能情况一一列举,再由古典概型的概率公式计算可得;
解:(1)由图知众数为![]()
∵![]()
∴平均数为![]()
(2)由图可得轻度拥堵的路段有![]() (个),
(个),
中度拥堵的路段有![]() (个),
(个),
重度拥堵的路段有![]() (个),
(个),
用分层抽样的方法,在上述的![]() 个路段共抽取
个路段共抽取![]() 个路段,则应从轻度拥堵、中度拥堵、重度拥堵的路段中分别抽取的个数为
个路段,则应从轻度拥堵、中度拥堵、重度拥堵的路段中分别抽取的个数为![]() .
.
记抽取的![]() 个轻度拥堵路段为
个轻度拥堵路段为![]() ,
,![]() 个中度拥堵路段为
个中度拥堵路段为![]() ,
,![]() 个重度拥堵的路段为
个重度拥堵的路段为![]() ,则从这
,则从这![]() 个路段中任取
个路段中任取![]() 个的所有可能情况为
个的所有可能情况为![]() 、
、![]() 、
、![]() 、
、![]() 、
、![]() 、
、![]() 、
、![]() 、
、![]() 、
、![]() 、
、![]() 、
、![]() 、
、![]() 、
、![]() 、
、![]() 、
、![]() 、
、![]() 、
、![]() 、
、![]() 、
、![]() 、
、![]() ,共
,共![]() 种情况,其中至少有
种情况,其中至少有![]() 个路段为中度拥堵的情况为
个路段为中度拥堵的情况为![]() 、
、![]() 、
、![]() 、
、![]() 、
、![]() 、
、![]() 、
、![]() 、
、![]() 、
、![]() 、
、![]() ,共
,共![]() 种.
种.
记至少有![]() 个路段为中度拥堵为事件
个路段为中度拥堵为事件![]() ,则
,则![]() .
.


 阅读快车系列答案
阅读快车系列答案科目:高中数学 来源: 题型:
【题目】设有关于x的一元二次方程![]() .
.
![]() 若a是从0,1,2三个数中任取的一个数,b是从0,1,2,3四个数中任取的一个数,求上述方程有实根的概率;
若a是从0,1,2三个数中任取的一个数,b是从0,1,2,3四个数中任取的一个数,求上述方程有实根的概率;
![]() 若a是从区间
若a是从区间![]() 任取的一个数,b是从区间
任取的一个数,b是从区间![]() 任取的一个数,求上述方程有实数的概率.
任取的一个数,求上述方程有实数的概率.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数![]() .
.
(1)求![]() 的单调递增区间.
的单调递增区间.
(2)在ΔABC中,角A,B,C所对的边分别为a,b,c,若f(A)=1,c=10,cosB=![]() ,求ΔABC的中线AD的长.
,求ΔABC的中线AD的长.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】定义在R上的函数f(x)满足![]() ,
,![]() .
.
(1)求函数f(x)的解析式;
(2)求函数g(x)的单调区间;
(3)给出定义:若s,t,r满足![]() ,则称s比t更接近于r,当x≥1时,试比较
,则称s比t更接近于r,当x≥1时,试比较![]() 和
和![]() 哪个更接近
哪个更接近![]() ,并说明理由.
,并说明理由.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】公元263年左右,我国数学家刘徽发现当圆内接正多边形的边数无限增加时,多边形面积可无限逼近圆的面积,并创立了“割圆术”.利用“割圆术”刘徽得到了圆周率精确到小数点后两位的近似值3.14,这就是著名的“徽率”.小华同学利用刘徽的“割圆术”思想在半径为1的圆内作正![]() 边形求其面积,如图是其设计的一个程序框图,则框图中应填入、输出
边形求其面积,如图是其设计的一个程序框图,则框图中应填入、输出![]() 的值分别为( )
的值分别为( )
(参考数据:![]() )
)

A. ![]() B.
B. ![]()
C. ![]() D.
D. ![]()
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】下表提供了某厂节能降耗技术改造后生产甲产品过程中记录的产量![]() (吨)与相应的生产能耗
(吨)与相应的生产能耗![]() (吨标准煤)的几组对照数据
(吨标准煤)的几组对照数据
| 3 | 4 | 5 | 6 |
| 2.5 | 3 | 4 | 4.5 |
(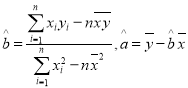 )
)
(1)请根据上表提供的数据,用最小二乘法求出![]() 关于
关于![]() 的线性回归方程
的线性回归方程![]() ;
;
(2)已知该厂技术改造前100吨甲产品能耗为90吨标准煤.试根据(1)求出的线性回归方程,预测生产100吨甲产品的生产能耗比技术改造前降低多少吨标准煤?
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】给出下列四个命题:
①命题“若![]() ,则
,则![]() ”的逆否命题;
”的逆否命题;
②“![]() ,使得
,使得![]() ”的否定是:“
”的否定是:“![]() ,均有
,均有![]() ”;
”;
③命题“![]() ”是“
”是“![]() ”的充分不必要条件;
”的充分不必要条件;
④![]() :
:![]() ,
,![]() :
:![]() ,
,![]() 且
且![]() 为真命题.
为真命题.
其中真命题的序号是________.(填写所有真命题的序号)
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】噪声污染已经成为影响人们身体健康和生活质量的严重问题,为了了解声音强度![]() (单位:分贝)与声音能量
(单位:分贝)与声音能量![]() (单位:
(单位:![]() )之间的关系,将测量得到的声音强度
)之间的关系,将测量得到的声音强度![]() 和声音能量
和声音能量![]() (
(![]() ,2,…,10)数据作了初步处理,得到如图散点图及一些统计量的值.
,2,…,10)数据作了初步处理,得到如图散点图及一些统计量的值.

|
|
|
|
|
|
|
|
|
|
|
|
|
|
表中![]() .
.
(1)根据散点图判断,![]() 与
与![]() 哪一个适宜作为声音强度
哪一个适宜作为声音强度![]() 关于声音能量
关于声音能量![]() 的回归方程类型?(给出判断即可,不必说明理由)
的回归方程类型?(给出判断即可,不必说明理由)
(2)根据表中数据,求声音强度关于声音能量的回归方程.
参考公式: ;
;![]()
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com