
【题目】函数y=cosπx的图象与函数y=( ![]() )|x﹣1|(﹣3≤x≤5)的图象所有交点的横坐标之和等于( )
)|x﹣1|(﹣3≤x≤5)的图象所有交点的横坐标之和等于( )
A.4
B.6
C.8
D.10
【答案】C
【解析】解:作出函数y=cosπx的图象,则函数关于x=1对称, 同时函数y=( ![]() )|x﹣1|(﹣3≤x≤5)也关于x=1对称,
)|x﹣1|(﹣3≤x≤5)也关于x=1对称,
由图象可知,两个函数在﹣3≤x≤5上共有8个交点,两两关于x=1对称,
设对称的两个点的横坐标分别为x1 , x2 ,
则x1+x2=2×1=2,
∴8个交点的横坐标之和为4×2=8.
故选:C.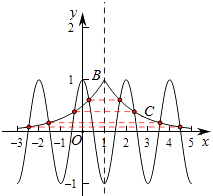
【考点精析】解答此题的关键在于理解函数的零点与方程根的关系的相关知识,掌握二次函数的零点:(1)△>0,方程 有两不等实根,二次函数的图象与 轴有两个交点,二次函数有两个零点;(2)△=0,方程 有两相等实根(二重根),二次函数的图象与 轴有一个交点,二次函数有一个二重零点或二阶零点;(3)△<0,方程 无实根,二次函数的图象与 轴无交点,二次函数无零点.


 黄冈创优卷系列答案
黄冈创优卷系列答案科目:高中数学 来源: 题型:
【题目】设数列{an}的前n项和为Sn满足2Sn=an+1﹣2n+1+1,n∈N* , 且a1 , a2+5,a3成等差数列.
(1)求a1的值;
(2)求数列{an}的通项公式.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知圆![]() 恰好经过椭圆
恰好经过椭圆![]() 的两个焦点和两个顶点.
的两个焦点和两个顶点.
(1)求椭圆![]() 的方程;
的方程;
(2)经过原点的直线![]() (不与坐标轴重合)交椭圆
(不与坐标轴重合)交椭圆![]() 于
于![]() 两点,
两点, ![]() 轴,垂足为
轴,垂足为![]() ,连接
,连接![]() 并延长
并延长![]() 交椭圆
交椭圆![]() 于
于![]() ,证明:以线段
,证明:以线段![]() 为直径的圆经过点
为直径的圆经过点![]() .
.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】等比数列{an}中,a2﹣a1=2,且2a2为3a1和a3的等差中项.
(1)求数列{an}的通项公式;
(2)设bn=2log3an+1,且数列{ ![]() }的前n项和为Tn . 求Tn .
}的前n项和为Tn . 求Tn .
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某校高一某班的一次数学测试成绩(满分为100分)的茎叶图和频率分布直方图都受到不同程度的破坏,但可见部分如图,据此解答如下问题; 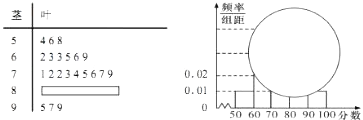
(1)求分数在[50,60)的频率及全班的人数;
(2)求分数在[80,90)之间的频数,并计算频率分布直方图中[80,90)间的矩形的高;
(3)根据频率分布直方图,估计该班数学成绩的平均数与中位数.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com