Question

已知全集U=R，集合A={a|关于x的方程x²+ax+1=0有实根}，集合B={a|关于x的方程ax²+x+1=0有实根}．求A∩B，A∪B，A∩（C_UB）．

Answer 1

解：由△₁=a²-4≥0可得a≤-2或a≥2，
故A={a|a≤-2或a≥2}．
当a=0时，方程x+1=0有实根；
当a≠0时，由△₂=1-4a≥0可得．
因此，
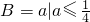
从而，
所以．
分析：由一元二次方程根的个数与△符号的关系，我们可以分别求出集合A={a|关于x的方程x²+ax+1=0有实根}和集合B={a|关于x的方程ax²+x+1=0有实根}．进而根据集合交集，并集及补集的定义，得到答案．
点评：本题考查的知识点是集合交、并、补的混合运算，其中根据一元二次方程根的个数与△符号的关系，构造关于a的不等式，求出集合A，B是解答本题的关键．