Question

【题目】已知函数f（x）=3x2+2（k﹣1）x+k+5．
（1）求函数f（x）在[0，3]上最大值；
（2）若函数f（x）在[0，3]上有零点，求实数k的取值范围．

Answer 1

【答案】
（1）解：由已知，函数f（x）的图象是开口向上的抛物线，对称轴为直线 ．

当 ，即 时，f（x）max=f（3）=7k+26．

当 ，即 时，f（x）max=f（0）=k+5．

综上： .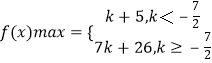

（2）解：1°当函数f（x）在[0，3]上有两相同的零点时： ，

解得k=﹣2．

2°当函数f（x）在[0，3]上有两不同的零点时： ，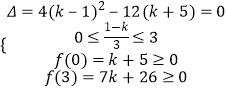

解得 .

3°当函数f（x）有两个不同零点且在[0，3]上仅有一个零点时：

由零点存在定理得：f（0）f（3）≤0，解得 ．

而当k=﹣5时，f（x）=3x2﹣12x，此时该函数的零点为0和4，符合要求．

综上：﹣5≤k≤﹣2.

解法2：函数f（x）在[0，3]上有零点等价于方程3x2+2（k﹣1）x+k+5=0在[0，3]上有解

即k（2x+1）=﹣（3x2﹣2x+5）

所以

令t=2x+1∈[1，7]，则 在[1，3]单调递增，在[3，7]单调递减

所以k∈[﹣5，﹣2]．

【解析】（1）由已知，函数f（x）的图象是开口向上的抛物线，对称轴为直线 ，分类讨论，即可求出函数f（x）在[0，3]上最大值；（2）分类讨论函数f（x）在区间[0，3]上有两相同的零点、两不同的零点、函数f（x）有两个不同零点且在[0，3]上仅有一个零点，根据函数性质组成不等式组求解即可．或利用分离参数求最值的方法求解．
【考点精析】本题主要考查了二次函数的性质的相关知识点，需要掌握当时，抛物线开口向上，函数在上递减，在上递增；当时，抛物线开口向下，函数在上递增，在上递减才能正确解答此题．