【答案】
分析:(I)当a=1时,f(x)=-x(x-1)
2=-x
3+2x
2-x,得f(2)=-2,且f′(x)=-3x
2+4x-1,f′(2)=-5.由此能求出曲线y=-x(x-1)
2在点(2,-2)处的切线方程.
(Ⅱ)f(x)=-x(x-a)
2=-x
3+2ax
2-a
2x,f′(x)=-3x
2+4ax-a
2=-(3x-a)(x-a).令f′(x)=0,解得x=
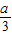
,或x=a.由a的符号进行分类讨论,能求出函数f(x)的极大值和极小值.
(Ⅲ)假设在区间[-1,0]上存在实数k满足题意.由a>3,得
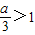
,当k∈[-1,0]时,k-cosx≤1,k
2-cos
2x≤1.由f(x)在(-∞,1]上是减函数,知要使f(k-cosx)≥f(k
2-cos
2x)≥f(k
2-cos
2x),x∈R,只要k-cosx≤k
2-cos
2x,(x∈R).由此能推导出在区间[-1,0]上存在k=-1,使得f(x-cosx)≥f(k
2-cos
2x)对任意的x∈R恒成立.…13分.
解答:解:(I)当a=1时,f(x)=-x(x-1)
2=-x
3+2x
2-x,得f(2)=-2,
且f′(x)=-3x
2+4x-1,f′(2)=-5.
所以,曲线y=-x(x-1)
2在点(2,-2)处的切线方程是y+2=-5(x-2),
整理得5x+y-8=0.…3分
(Ⅱ)f(x)=-x(x-a)
2=-x
3+2ax
2-a
2x,
f′(x)=-3x
2+4ax-a
2=-(3x-a)(x-a).
令f′(x)=0,解得x=
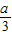
,或x=a.
由于a≠0,以下分两种情况讨论.
(1)若a>0,当变化时,f′(x)的正负如下表:
| x | (-∞,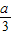 ) ) | 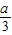 | (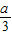 ,a) ,a) | a | (a,+∞) |
| f′(x) | ↓ | | ↑ | | ↓ |
因此,函数f(x)在x=
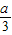
处取得极小值f(
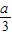
),且f(

)=-
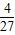
a
3;
函数f(x)在x=a处取得极大值f(a),且f(a)=0.…5分
(2)若a<0,当变化时,f′(x)的正负如下表:
因此,函数f(x)在x=a处取得极小值f(a),且f(a)=0;
函数f(x)在x=
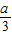
处取得极大值f(
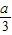
),且f(
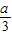
)=-
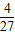
a
3. …8分
(Ⅲ)假设在区间[-1,0]上存在实数k满足题意.
由a>3,得
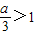
,当k∈[-1,0]时,k-cosx≤1,
k
2-cos
2x≤1.
由(Ⅱ)知,f(x)在(-∞,1]上是减函数,
要使f(k-cosx)≥f(k
2-cos
2x)≥f(k
2-cos
2x),x∈R
只要k-cosx≤k
2-cos
2x,(x∈R)
即cos
2x-cosx≤k
2-k,(x∈R)①
设g(x)=cos
2x-cosx=(cosx-

)
2-

,则函数g(x)在R上的最大值为-

.
要使①式恒成立,必须k
2-k≥2,即k≥2,或k≤-1.
所以,在区间[-1,0]上存在k=-1,
使得f(x-cosx)≥f(k
2-cos
2x)对任意的x∈R恒成立.…13分.
点评:本题考查曲线的切线方程式的求法,考查函数的极大值和极小值的求法,探索满足条件的实数值的求法.解题时要认真审题,注意分类讨论思想和等价转化思想的合理运用.

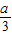 ,或x=a.由a的符号进行分类讨论,能求出函数f(x)的极大值和极小值.
,或x=a.由a的符号进行分类讨论,能求出函数f(x)的极大值和极小值.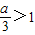 ,当k∈[-1,0]时,k-cosx≤1,k2-cos2x≤1.由f(x)在(-∞,1]上是减函数,知要使f(k-cosx)≥f(k2-cos2x)≥f(k2-cos2x),x∈R,只要k-cosx≤k2-cos2x,(x∈R).由此能推导出在区间[-1,0]上存在k=-1,使得f(x-cosx)≥f(k2-cos2x)对任意的x∈R恒成立.…13分.
,当k∈[-1,0]时,k-cosx≤1,k2-cos2x≤1.由f(x)在(-∞,1]上是减函数,知要使f(k-cosx)≥f(k2-cos2x)≥f(k2-cos2x),x∈R,只要k-cosx≤k2-cos2x,(x∈R).由此能推导出在区间[-1,0]上存在k=-1,使得f(x-cosx)≥f(k2-cos2x)对任意的x∈R恒成立.…13分.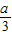 ,或x=a.
,或x=a.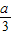 )
)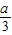
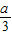 ,a)
,a)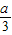 处取得极小值f(
处取得极小值f(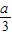 ),且f(
),且f( )=-
)=-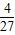 a3;
a3;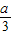 )
)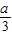
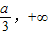 )
)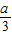 处取得极大值f(
处取得极大值f(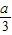 ),且f(
),且f(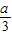 )=-
)=-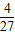 a3. …8分
a3. …8分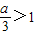 ,当k∈[-1,0]时,k-cosx≤1,
,当k∈[-1,0]时,k-cosx≤1, )2-
)2- ,则函数g(x)在R上的最大值为-
,则函数g(x)在R上的最大值为- .
.
