
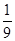 =-2,所以f(log3
=-2,所以f(log3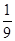 )=f(-2)=-f(2),
)=f(-2)=-f(2),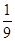 ),即:b<a<c
),即:b<a<c

 新题型全程检测期末冲刺100分系列答案
新题型全程检测期末冲刺100分系列答案科目:高中数学 来源: 题型:
已知函数y=f(x)与函数y=![]() +
+![]() 是相等的函数,则函数y=f(x)的定义域是 ( )
是相等的函数,则函数y=f(x)的定义域是 ( )
A.[-3,1] B.(-3,1)
C.(-3,+∞) D.(-∞,1]
查看答案和解析>>
科目:高中数学 来源:2012年人教A版高中数学必修四1.6三角函数模型的简单应用练习卷(解析版) 题型:选择题
已知函数y=f(x)的图象如图所示,则函数y=f sinx在[0,π]上的大致图象是( )
sinx在[0,π]上的大致图象是( )



查看答案和解析>>
科目:高中数学 来源:2011-2012学年广东省肇庆市高三复习必修一数学(B) 题型:解答题
(本题满分12分)已知函数y=f(x)是R上的偶函数,且x≥0时,f(x)=( )x-1.
)x-1.
(1)求f(x)的解析式;
(2)画出此函数的图象.
查看答案和解析>>
科目:高中数学 来源:2010-2011学年江西省高三下学期第一次月考数学文卷 题型:填空题
.已知函数y=f(x)是偶函数,当x>0时,f(x)=x+,且当x∈[-3,- 1]时,n≤f(x)≤m恒成立,则m-n的最小值是__________.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com