
【题目】已知集合A={x|x2﹣ax+a2﹣19=0},集合B={x|x2﹣5x+6=0},C={x|x2+2x﹣8=0}.
(1)若A∩B=A∪B,求a的值;
(2)若A∩B,A∩C=,求a的值.
【答案】
(1)解:∵集合B={x|x2﹣5x+6=0}={2,3},
又∵A∩B=A∪B,
∴集合A={x|x2﹣ax+a2﹣19=0}={2,3},
则2+3=a,
即a=5
(2)解:集合C={x|x2+2x﹣8=0}={﹣4,2}.
∵A∩B,A∩C=,
∴3∈A,2A;
∴9﹣3a+a2﹣19=0,4﹣2a+a2﹣19≠0;
解得,a=﹣2
【解析】(1)由A∩B=A∪B,可知A=B,由题意求出B,用韦达定理求a;(2)由A∩B,A∩C=,又∵B={2,3},C={2,﹣4};则3∈A,2A;解出a即可.
【考点精析】利用集合的并集运算和集合的交集运算对题目进行判断即可得到答案,需要熟知并集的性质:(1)A![]() A∪B,B
A∪B,B![]() A∪B,A∪A=A,A∪
A∪B,A∪A=A,A∪![]() =A,A∪B=B∪A;(2)若A∪B=B,则A
=A,A∪B=B∪A;(2)若A∪B=B,则A![]() B,反之也成立;交集的性质:(1)A∩B
B,反之也成立;交集的性质:(1)A∩B![]() A,A∩B
A,A∩B![]() B,A∩A=A,A∩
B,A∩A=A,A∩![]() =
=![]() ,A∩B=B∩A;(2)若A∩B=A,则A
,A∩B=B∩A;(2)若A∩B=A,则A![]() B,反之也成立.
B,反之也成立.


 阅读快车系列答案
阅读快车系列答案科目:高中数学 来源: 题型:
【题目】给定 ![]() ,设函数
,设函数 ![]() 满足:对于任意大于
满足:对于任意大于 ![]() 的正整数
的正整数 ![]() ,
, ![]()
(1)设 ![]() ,则其中一个函数
,则其中一个函数 ![]() 在
在 ![]() 处的函数值为;
处的函数值为;
(2)设 ![]() ,且当
,且当 ![]() 时,
时, ![]() ,则不同的函数
,则不同的函数 ![]() 的个数为。
的个数为。
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】设集合A={x|x2+2x﹣3<0},集合B={x||x+a|<1}.
(1)若a=3,求A∪B;
(2)设命题p:x∈A,命题q:x∈B,若p是q成立的必要不充分条件,求实数a的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】盒中有标号分别为0,1,2,3的球各一个,这些球除标号外均相同.从盒中依次摸取两个球(每次一球,摸出后不放回),记为一次游戏.规定:摸出的两个球上的标号之和等于5为一等奖,等于4为二等奖,等于其它为三等奖.
(1)求完成一次游戏获三等奖的概率;
(2)记完成一次游戏获奖的等级为ξ,求随机变量ξ的分布列和数学期望.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,在正方体ABCD-A1B1C1D1中,O为底面ABCD的中心,P是DD1的中点,设Q是CC1上的点,问:当点Q在什么位置时,平面D1BQ与平面PAO平行?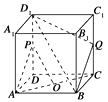
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com