
【题目】有3名男生、4名女生,在下列不同条件下,求不同的排列方法总数.
(1)选5人排成一排;
(2)排成前后两排,前排4人,后排3人;
(3)全体排成一排,甲不站排头也不站排尾;
(4)全体排成一排,女生必须站在一起;
(5)全体排成一排,男生互不相邻.
【答案】(1)2520种(2)5040种(3)3600种(4)576种(5)1440种
【解析】
(1)按照排列的定义求解..
(2)分两步完成,先选4人站前排进行排列,余下3人站后排进行排列,然后相乘求解..
(3)先考虑甲,再其余6人进行排列,然后相乘求解.
(4)将女生看作一个整体与3名男生一起全排列,再将女生全排列,然后相乘求解.
(5)先排女生,再在女生之间及首尾5个空位中任选3个空位安排男生,然后相乘求解.
(1)从7人中选5人排列,有![]() (种).
(种).
(2)分两步完成,先选4人站前排,有![]() 种方法,余下3人站后排,有
种方法,余下3人站后排,有![]() 种方法,共有
种方法,共有![]() (种).
(种).
(3)(特殊元素优先法)先排甲,有5种方法,其余6人有![]() 种排列方法,共有
种排列方法,共有![]() (种).
(种).
(4)(捆绑法)将女生看作一个整体与3名男生一起全排列,有![]() 种方法,再将女生全排列,有
种方法,再将女生全排列,有![]() 种方法,共有
种方法,共有![]() (种).
(种).
(5)(插空法)先排女生,有![]() 种方法,再在女生之间及首尾5个空位中任选3个空位安排男生,有
种方法,再在女生之间及首尾5个空位中任选3个空位安排男生,有![]() 种方法,共有
种方法,共有![]() (种).
(种).


科目:高中数学 来源: 题型:
【题目】某校进行了一次创新作文大赛,共有100名同学参赛,经过评判,这100名参赛者的得分都在![]() 之间,其得分的频率分布直方图如图,则下列结论错误的是
之间,其得分的频率分布直方图如图,则下列结论错误的是
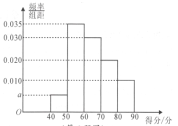
A. 得分在![]() 之间的共有40人
之间的共有40人
B. 从这100名参赛者中随机选取1人,其得分在![]() 的概率为
的概率为![]()
C. 这100名参赛者得分的中位数为65
D. 估计得分的众数为55
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】
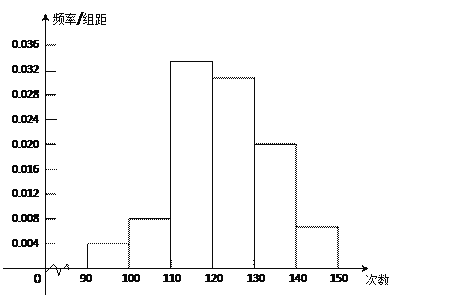
为了了解高中新生的体能情况,某学校抽取部分高一学生进行一分钟跳绳次数测试,将所得数据整理后,画出频率分布直方图(如图),图中从 左到右各小长方形面积之比为2:4:17:15:9:3,第二小组频数为12﹒
[来
(Ⅰ)第二小组的频率是多少?样本容量是多少?
(Ⅱ)若次数在110以上(含110次)为达标,试估计该学校全体高一学生的达标率是多少?
(Ⅲ)在这次测试中,学生跳绳次数的中位数落在哪个小组内?请说明理由.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】现安排甲、乙、丙、丁、戊5名同学参加2022年杭州亚运会志愿者服务活动,有翻译、导游、礼仪、司机四项工作可以安排,以下说法正确的是( )
A.每人都安排一项工作的不同方法数为54
B.每人都安排一项工作,每项工作至少有一人参加,则不同的方法数为![]()
C.如果司机工作不安排,其余三项工作至少安排一人,则这5名同学全部被安排的不同方法数为![]()
D.每人都安排一项工作,每项工作至少有一人参加,甲、乙不会开车但能从事其他三项工作,丙、丁、戊都能胜任四项工作,则不同安排方案的种数是![]()
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某工厂生产某种产品的年固定成本为250万元,每生产x千件,需另投入成本为C(x),当年产量不足80千件时,C(x)=![]() x2+10x(万元).当年产量不小于80千件时,C(x)=51x+
x2+10x(万元).当年产量不小于80千件时,C(x)=51x+![]() -1 450(万元).每件商品售价为0.05万元.通过市场分析,该厂生产的商品能全部售完.
-1 450(万元).每件商品售价为0.05万元.通过市场分析,该厂生产的商品能全部售完.
(1)写出年利润L(x)(万元)关于年产量x(千件)的函数解析式;
(2)当年产量为多少千件时,该厂在这一商品的生产中所获利润最大?
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图所示,位于A处的信息中心获悉:在其正东方向相距40海里的B处有一艘渔船遇险,在原地等待营救.信息中心立即把消息告知在其南偏西30°,相距20海里的C处的乙船,现乙船朝北偏东![]() 的方向即沿直线CB前往B处救援,则
的方向即沿直线CB前往B处救援,则![]() 等于 ( )
等于 ( )

A. ![]() B.
B. ![]() C.
C. ![]() D.
D. ![]()
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知在平面直角坐标系![]() 中,曲线
中,曲线![]() 的参数方程为
的参数方程为![]() (
(![]() 为参数),以
为参数),以![]() 轴的非负半轴为极轴,原点
轴的非负半轴为极轴,原点![]() 为极点建立极坐标系,两种坐标系中取相同的长度单位,若直线
为极点建立极坐标系,两种坐标系中取相同的长度单位,若直线![]() 和
和![]()
![]() 分别与曲线
分别与曲线![]() 相交于
相交于![]() 、
、![]() 两点(
两点(![]() ,
,![]() 两点异于坐标原点).
两点异于坐标原点).
(1)求曲线![]() 的普通方程与
的普通方程与![]() 、
、![]() 两点的极坐标;
两点的极坐标;
(2)求直线![]() 的极坐标方程及
的极坐标方程及![]() 的面积.
的面积.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com