
����Ŀ��ij�н����ڸ���һ��ͨ��ǰ���Թ����ij������г�飬����һ���ij�飬������ƺ�ݳ���60����ͼ�����þƾ������Ƕ���60 ���ƺ�ݳ���ѪҺ�оƾ�Ũ�Ƚ��м��������ý��������Ƶ�ʷֲ�ֱ��ͼ��


��1��ͳ�Ʒ����У�ͬһ�����ݳ��ø���������е�ֵ��Ϊ������ͼ�ҵij����ͼ�Ƕ���60���ƺ�ݳ���ѪҺ�ľƾ�Ũ������һ����ͳ�ƣ����ͼ�������Sֵ����˵��S��ͳ�����壻��ͼ��������![]() ��
��![]() �ֱ��ʾͼ���и��������ֵ��Ƶ�ʣ�
�ֱ��ʾͼ���и��������ֵ��Ƶ�ʣ�
��2�������ж��У��⡢����λ���������ƾ������Dz�þƾ�Ũ������![]() �ķ�Χ�����������û����ô�࣬�Dz����Dz���������Ӷӳ������ڱ��ƾ������Dz�þƾ�Ũ������
�ķ�Χ�����������û����ô�࣬�Dz����Dz���������Ӷӳ������ڱ��ƾ������Dz�þƾ�Ũ������![]() ��Χ�ľƺ�ݳ�����������2�˳�Ѫ���飬
��Χ�ľƺ�ݳ�����������2�˳�Ѫ���飬 ![]() Ϊ�⡢����λ���������е���������
Ϊ�⡢����λ���������е���������![]() �ķֲ��У������⡢����λ����������1�˱����еĸ��ʣ�
�ķֲ��У������⡢����λ����������1�˱����еĸ��ʣ�
��3���ܶ����ںȾƺ�ͨ���Ȳ轵�����ھƾ�Ũ�ȣ�����ʱ�����ָ���ƺ�Ȳ�����. Ϊ�о����ھƺ�Ȳ����������Ƿ��йأ�ij���л����ɼ���ͳ���������±����������������ʵĽǶ������жϽ������˵������.
û�������� | �������� | |
���ھƺ�Ȳ� | 2099 | 49 |
�ƺȲ� | 7775 | 42 |
���𰸡���1��47����2��![]() ����3���й�
����3���й�
�������������������1����ͼ��֪�����![]() ��������֪���ݿ���2������ֱ��ͼ����ƾ�Ũ������
��������֪���ݿ���2������ֱ��ͼ����ƾ�Ũ������![]() �ķ�Χ��������Ȼ�����
�ķ�Χ��������Ȼ����� ![]() ȡֵ�����������Ӧ�ĸ��ʣ��������ֲ��У���3������ڳ��ھƺ�Ȳ���������������˵ĸ��ʼ��ھƺȲ���������������˵ĸ��ʣ��Ƚ�
ȡֵ�����������Ӧ�ĸ��ʣ��������ֲ��У���3������ڳ��ھƺ�Ȳ���������������˵ĸ��ʼ��ھƺȲ���������������˵ĸ��ʣ��Ƚ�![]() ��
��![]() �Ĺ�ϵ�������жϳ����.
�Ĺ�ϵ�������жϳ����.
�����������1����ͼ��֪�����![]() =
=
![]() ��47��mg/100ml����S��ͳ������Ϊ60���ƺ�ݳ���ѪҺ�ľƾ�Ũ�ȵ�ƽ��ֵ.
��47��mg/100ml����S��ͳ������Ϊ60���ƺ�ݳ���ѪҺ�ľƾ�Ũ�ȵ�ƽ��ֵ.
��2���ƾ�Ũ������70��90![]() �ķ�Χ������Ϊ
�ķ�Χ������Ϊ![]() ��
�� ![]() ȡֵΪ0��1��2��
ȡֵΪ0��1��2�� ![]() ��
�� ![]() ��
�� ![]()
![]() �ķֲ������£�
�ķֲ������£�
| 0 | 1 | 2 |
P |
|
|
|
�⡢����λ����������1�˱����еĸ���![]()
![]() ��
��
��3���жϽ�������ھƺ�Ȳ����������йأ��ڳ��ھƺ�Ȳ���������������˵ĸ���Ϊ![]() �ھƺȲ���������������˵ĸ���Ϊ
�ھƺȲ���������������˵ĸ���Ϊ![]() �������ƺ�Ȳ��������ˡ��أ���
�������ƺ�Ȳ��������ˡ��أ���![]() ����
����![]() ��
��![]() ���϶࣬����Ӧ���й�.
���϶࣬����Ӧ���й�.


 ��������һ���þ�ϵ�д�
��������һ���þ�ϵ�д� Сѧ��10����Ӧ����ϵ�д�
Сѧ��10����Ӧ����ϵ�д�
| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ��������[��1��1]�ϵĺ���f��x�����㣺�ٶ�����a��b��[��1��1]����a+b��0������ ![]() ��0��������f��x����[��1��1]�����溯������f��1��=1��
��0��������f��x����[��1��1]�����溯������f��1��=1��
��1����֤��f��x����[��1��1]���ǵ�������������
��2�������x����ʽf��x����f�� ![]() x+1����
x+1����
��3����f��x����m2��2am��2�����е�x��[��1��1]��a��[��1��1]���������ʵ��m��ȡֵ��Χ��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ��Ϊ�˷���ij������ѧ����ѧϰ״̬��������һ�ε�ѧϰ�ṩָ���Խ��飮�ֶ���ǰ![]() �ο��Ե���ѧ�ɼ�
�ο��Ե���ѧ�ɼ�![]() �������ɼ�
�������ɼ�![]() ���з����������Ǹ���
���з����������Ǹ���![]() �ο��Եijɼ���
�ο��Եijɼ���
88 | 83 | 117 | 92 | 108 | 100 | 112 | |
���� | 94 | 91 | 108 | 96 | 104 | 101 | 106 |
��1��������ѧ�ɼ��������ɼ��ĸ����ȶ��������������ɣ�
��2����֪�����������ɼ�![]() ����ѧ�ɼ�
����ѧ�ɼ�![]() ��������صģ��������������ɼ��ﵽ
��������صģ��������������ɼ��ﵽ![]() �֣��������������ѧ�ɼ���Լ�Ƕ��٣�
�֣��������������ѧ�ɼ���Լ�Ƕ��٣�
���ο���ʽ�� 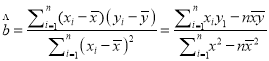 ��
�� ![]() ��
��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����֪����f��x��=lg��2+x����g��x��=lg��2��x������h��x��=f��x��+g��x��
��1������h��x���Ķ�����
��2���жϺ���h��x������ż�ԣ���˵�����ɣ�
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����12����ijУ�ס��������༶����5�����Ϊ1��2��3��4��5��ѧ������Ͷ��ѵ����ÿ��Ͷ10�Σ�Ͷ�еĴ���ͳ�����±���
ѧ�� | 1�� | 2�� | 3�� | 4�� | 5�� |
�װ� | 6 | 5 | 7 | 9 | 8 |
�Ұ� | 4 | 8 | 9 | 7 | 7 |
��1����ͳ�����ݿ����������������ĸ���ɼ����ȶ�������������˵������
��2�������ϱ�������Ϊѧ��Ͷ�������ʣ��涨�����༶��1�ź�2��ͬѧ�ֱ�����Լ��İ༶�μӱ�����ÿ��Ͷ��һ�Σ����ס�������������ͬѧͶ�еĴ���֮�ͷֱ����![]() ��
��![]() ������
������![]() ��
��![]() �ķֲ��к���ѧ������
�ķֲ��к���ѧ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ��������z=1+i��i��������λ������ ![]() +z2��ֵ�� ������x��y��R������z=x+yi��������|z|2+��z+
+z2��ֵ�� ������x��y��R������z=x+yi��������|z|2+��z+ ![]() ��i=
��i= ![]() ������x��y��ֵ��
������x��y��ֵ��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����֪0������ ![]() ��cos��2�Щ�������sin���Щ�����=��
��cos��2��������sin��������=�� ![]()
��1����sin��+cos����ֵ��
��2����sin��2���� ![]() ����ֵ��
����ֵ��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����֪����f��x��=exsinx������x��R��e=2.71828��Ϊ��Ȼ�����ĵ����� ��������f��x���ĵ������䣻
���� ![]() ʱ��f��x����kx����ʵ��k��ȡֵ��Χ��
ʱ��f��x����kx����ʵ��k��ȡֵ��Χ��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����f��x��=ax3+bx2+cx�ļ�СֵΪ��8���䵼����y=f�䣨x����ͼ���� ![]() ����ͼ��ʾ��
����ͼ��ʾ�� 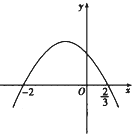
��1����f��x���Ľ���ʽ��
��2������x��[��3��3]����f��x����m2��14m���������ʵ��m��ȡֵ��Χ��
�鿴�𰸺ͽ���>>
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com