
【题目】已知双曲线![]() (
(![]() ,
,![]() ),
),![]() ,
,![]() 是双曲线的两个顶点,
是双曲线的两个顶点,![]() 是双曲线上的一点,且与点
是双曲线上的一点,且与点![]() 在双曲线的同一支上,
在双曲线的同一支上,![]() 关于
关于![]() 轴的对称点是
轴的对称点是![]() ,若直线
,若直线![]() ,
,![]() 的斜率分别是
的斜率分别是![]() ,
,![]() ,且
,且![]() ,则双曲线的离心率是( )
,则双曲线的离心率是( )
A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
 全能测控一本好卷系列答案
全能测控一本好卷系列答案科目:高中数学 来源: 题型:
【题目】设关于x的方程x2﹣ax﹣1=0和3x2﹣6x+3﹣2a=0的实根分别为x1,x2和x3,x4.若x1<x3<x2<x4,则实数a的取值范围为_____.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】己知函数![]() .
.
(1)试讨论f(x)的单调性;
(2)若函数![]() 有且只有三个不同的零点,分别记为x1,x2,x3,设x1<x2<x3,且
有且只有三个不同的零点,分别记为x1,x2,x3,设x1<x2<x3,且![]() 的最大值是e2,求x1x3的最大值.
的最大值是e2,求x1x3的最大值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,直三棱柱ABC﹣A1B1C1,中,点M是棱BC的中点.
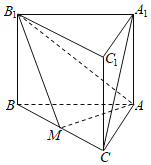
(2)求证:A1C∥平面AB1M;
(2)如果AB=AC,求证AM⊥平面BCC1B1.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】“2019曹娥江国际马拉松”在上虞举行,现要选派5名志愿者服务于![]() 四个不同的运动员救助点,每个救助点至少分配1人,若志愿者甲要求不到A救助点,则不同的分派方案有________种.
四个不同的运动员救助点,每个救助点至少分配1人,若志愿者甲要求不到A救助点,则不同的分派方案有________种.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】4支足球队进行单循环比赛(任两支球队恰进行一场比赛),任两支球队之间胜率都是![]() .单循环比赛结束,以获胜的场次数作为该队的成绩,成绩按从大到小排名次顺序,成绩相同则名次相同.下列结论中正确的是( )
.单循环比赛结束,以获胜的场次数作为该队的成绩,成绩按从大到小排名次顺序,成绩相同则名次相同.下列结论中正确的是( )
A.恰有四支球队并列第一名为不可能事件B.有可能出现恰有三支球队并列第一名
C.恰有两支球队并列第一名的概率为![]() D.只有一支球队名列第一名的概率为
D.只有一支球队名列第一名的概率为![]()
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在某校矩形的航天知识竞赛中,参与竞赛的文科生与理科生人数之比为1:3,且成绩分布在![]() 范围内,规定分数在80以上(含80)的同学获奖,按文理科用分层抽样的放发抽取200人的成绩作为样本,得到成绩的频率分布直方图.
范围内,规定分数在80以上(含80)的同学获奖,按文理科用分层抽样的放发抽取200人的成绩作为样本,得到成绩的频率分布直方图.
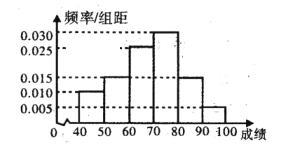
(Ⅰ)填写下面![]() 的列联表,能否有超过95%的把握认为“获奖与学生的文理科有关”;
的列联表,能否有超过95%的把握认为“获奖与学生的文理科有关”;
(Ⅱ)将上述调查所得的频率视为概率,现从参赛学生中,任意抽取3名学生,记“获奖”学生人数为![]() ,求
,求![]() 的分布列及数学期望.
的分布列及数学期望.

附表及公式:![]() ,其中
,其中![]()

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com