分析:(1)连接AC,B
1D
1,AC∩BD=O,A
1C
1∩B
1D
1=O
1,连接D
1O,O
1B,则可证D
1O∥面A
1C
1B,即可得到结论;
(2)连接B
1D,则B
1D⊥面A
1C
1B,设垂足为G,则∠GBB
1为直线BB
1和面A
1C
1B所成角,即可求解;
(3)△A
1C
1B在底面ABCD中的射影为△ACB,则面A
1C
1B与底面ABCD所成二面角的平面角的余弦值为
,从而可得结论.
解答:
解:(1)连接AC,B
1D
1,AC∩BD=O,A
1C
1∩B
1D
1=O
1,连接D
1O,O
1B,则
∵D
1O
1=BO,D
1O
1∥BO,∴四边形D
1OBO
1是平行四边形,
∴D
1O∥O
1B
∵D
1O?平面A
1C
1B,O
1B?平面A
1C
1B,
∴D
1O∥面A
1C
1B;
∴BD上存在中点E,使D
1E∥面A
1C
1B;
(2)连接B
1D,则B
1D⊥面A
1C
1B,设垂足为G,则∠GBB
1为直线BB
1和面A
1C
1B所成角
∵B
1G=
B
1D=
BB
1,
∴直线BB
1和面A
1C
1B所成角的正弦值为
;
(3)∵△A
1C
1B在底面ABCD中的射影为△ACB
∴面A
1C
1B与底面ABCD所成二面角的平面角的余弦值为
=
∴面A
1C
1B与底面ABCD所成二面角的平面角的正弦值
.
点评:本题考查线面平行,考查线面角,面面角,考查学生分析解决问题的能力,属于中档题.

 如图,正方体AC1
如图,正方体AC1 解:(1)连接AC,B1D1,AC∩BD=O,A1C1∩B1D1=O1,连接D1O,O1B,则
解:(1)连接AC,B1D1,AC∩BD=O,A1C1∩B1D1=O1,连接D1O,O1B,则

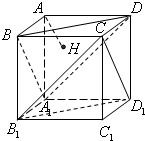 如图,正方体AC1的棱长为1,过点A作平面A1BD的垂线,垂足为点H.有下列四个命题:
如图,正方体AC1的棱长为1,过点A作平面A1BD的垂线,垂足为点H.有下列四个命题: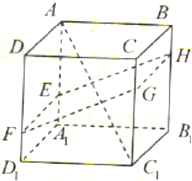 如图,正方体AC1中,
如图,正方体AC1中,