练习册

  • 练习册
  • 试题
    精英家教网 > 高中数学 > 题目详情

    【题目】如图，已知一艘海监船O上配有雷达，其监测范围是半径为25 km的圆形区域，一艘外籍轮船从位于海监船正东40 km的A处出发，径直驶向位于海监船正北30 km的B处岛屿，速度为28 km/h.

    问：这艘外籍轮船能否被海监船监测到？若能，持续时间多长？(要求用坐标法)

    【答案】解:如图，

    以O为原点，东西方向为x轴建立直角坐标系，则A(40,0)，B(0,30)，圆O方程x2＋y2＝252.

    直线AB方程： ＝1，即3x＋4y－120＝0.

    设O到AB距离为d，则d＝ ＝24<25，

    所以外籍轮船能被海监船监测到．

    设监测时间为t，则t＝ (h)

    答：外籍轮船能被海监船监测到，时间是0.5 h.


    【解析】先建立适合的坐标系，再求得点A，B所在直线的方程与海监船O监测范围边界所在圆的方程，那么直线AB与圆O所交弦长即为外籍轮船被监测的距离，除以外籍轮船的速度即为被监测的时间.

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：高中数学 来源： 题型：

    【题目】已知函数f（x）=x﹣ ﹣2alnx（a∈R） （Ⅰ）若函数f（x）在x=2时取极值，求实数a的值；
    （Ⅱ）若f（x）≥0对任意x∈[1，+∞）恒成立，求实数a的取值范围．

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】在棱长为2的正方体ABCD﹣A1B1C1D1中，P为底面正方形ABCD内一个动点，Q为棱AA1上的一个动点，若|PQ|=2，则PQ的中点M的轨迹所形成图形的面积是（ ）
    A.
    B.
    C.3
    D.4π

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】在如图所示的几何体中， 是 的中点， ．

    （1）已知 ， ，求证： 平面 ；
    （2）已知 分别是 和 的中点，求证： 平面 ．

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】已知中心在原点的椭圆与双曲线有公共焦点，左、右焦点分别为F1、F2 ， 且两条曲线在第一象限的交点为P，△PF1F2是以PF1为底边的等腰三角形．若|PF1|=10，椭圆与双曲线的离心率分别为e1、e2 ， 则e1e2+1的取值范围为（ ）
    A.（1，+∞）
    B.（ ，+∞）
    C.（ ，+∞）
    D.（ ，+∞）

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】已知圆O1的方程为x2＋(y＋1)2＝4，圆O2的圆心为O2(2,1)．
    （1）若圆O1与圆O2外切，求圆O2的方程；
    （2）若圆O1与圆O2交于A ， B两点，且|AB|＝2 ，求圆O2的方程．

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】已知三棱柱ABC﹣A1B1C1的侧棱与底面垂直，体积为 ，底面是边长为 的正三角形．若P为底面A1B1C1的中心，则PA与平面ABC所成角的大小为（ ）
    A.120°
    B.60°
    C.45°
    D.30°

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】已知数列{an}、{bn}都是公差为1的等差数列，其首项分别为a1、b1 ， 且a1+b1=5，a1 ， b1∈N* ， 设cn=a ，则数列{cn}的前10项和等于（ ）
    A.55
    B.70
    C.85
    D.100

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】设函数f（x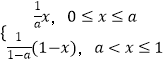）= ，a为常数，且a∈（0，1）．
    （1）若x0满足f（x0）=x0 ， 则称x0为f（x）的一阶周期点，证明函数f（x）有且只有两个一阶周期点；
    （2）若x0满足f（f（x0））=x0 ， 且f（x0）≠x0 ， 则称x0为f（x）的二阶周期点，当a= 时，求函数f（x）的二阶周期点．

    查看答案和解析>>

    同步练习册答案