
����Ŀ����֪��ԲQ������F��0����1��������ֱ��y=1���У���ԲN�ĶԳ���Ϊ�����ᣬ����Ϊ����ԭ��O��F����һ�����㣬�ֵ㣨0��2������ԲN�ϣ�
��1����ԲԲ��Q�Ĺ켣M�ķ��̺���ԲN�ķ��̣�
��2�����㣨0����4����ֱ��l���켣M��A��B���㣬����OA��OB������OA��OB����ԲN��C��D���㣬���OCD�������Сֵ��
��3�������⣺����ԲN��һ����P��Բx2+��y��1��2=1���������ߣ��е�ֱ�ΪG��H���� ![]() ��ȡֵ��Χ��
��ȡֵ��Χ��
���𰸡�
��1���⣺�����⣬�������ߵĶ����ö���Q�Ĺ켣M�ı�����Ϊ��x2=��4y��
�����������ԲN�ı�����Ϊ ![]() +
+ ![]() =1��a��b��0����
=1��a��b��0����
��Ȼ��c=1��a=2��b= ![]() ��
��
����ԲN�ı�����Ϊ�� ![]() ��
��
�켣 ![]()
��2���⣺ 
����x1x2+y1y2=0OA��OB
�� ![]() ��
��
���� ![]() ��
��
ͬ���ɵã� ![]() ��
��
���� ![]() ��
��
��t=1+k2��t��1���� 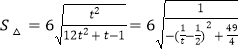 ��
��
���Ե� ![]()
��3���⣺���GPH=2����Բx2+��y��1��2=1��Բ��ΪE����ͼ��
��P����Բ�϶���ʱPE��СΪ1������Բ�¶���ʱ��|PE|�����ֵΪ3��PE��[1��3]��
PEcos��=PG��sin��= ![]() ��
��
�� 
= 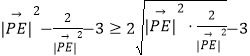 =
= ![]() �����ҽ���|PE|=
�����ҽ���|PE|= ![]() ʱȡ�Ⱥţ�
ʱȡ�Ⱥţ�
��Ϊ|PE|��[1��3]������ ![]() ��
��
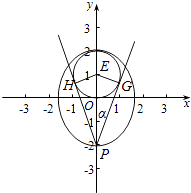
����������1���������ߵĶ���ɵö���Q�Ĺ켣M�ı����̣�������ɵ�c=1��a=2�����b�������õ���Բ���̣���2����Ȼֱ��m��б�ʴ��ڣ�������ֱ��m��ֱ�߷���Ϊ��y=kx��4���ֱ���������߷��̺���Բ���̣�����Τ�ﶨ�����ҳ���ʽ���Լ��㵽ֱ�ߵľ��빫ʽ����������ε���������ɲ���ʽ�����ʣ����ɵõ�������Сֵ����3�����EPF=2������� ![]() ����ʽ������
����ʽ������ ![]() �ķ�Χ��������ʽ�ķ�Χ���ɣ�
�ķ�Χ��������ʽ�ķ�Χ���ɣ�
�����㾫����������Ҫ��������Բ�ı����̵����֪ʶ�㣬��Ҫ������Բ�����̽�����x�![]() ��������y�
��������y�![]() ������ȷ�����⣮
������ȷ�����⣮


 ȫ��������ϵ�д�
ȫ��������ϵ�д� һ��һ����ʱ���ϵ�д�
һ��һ����ʱ���ϵ�д�
| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ��ʾ��һ��Բ����ƹ����Ͳ����Ϊ![]() ���ף�����뾶Ϊ
���ף�����뾶Ϊ![]() ����.��Ͳ���ϵ��µֱ�ճ��һ��ƹ����ƹ��������Ͳ���漰��������У���Ͳ��ƹ�����Ⱥ��Բ��ƣ�.һ��ƽ������ƹ��������У��Ҵ�ƽ�����Ͳ��Ե���õ�ͼ��Ϊһ����Բ�������Բ��������Ϊ�� ��
����.��Ͳ���ϵ��µֱ�ճ��һ��ƹ����ƹ��������Ͳ���漰��������У���Ͳ��ƹ�����Ⱥ��Բ��ƣ�.һ��ƽ������ƹ��������У��Ҵ�ƽ�����Ͳ��Ե���õ�ͼ��Ϊһ����Բ�������Բ��������Ϊ�� ��
![]()
A. ![]() B.
B. ![]() C.
C. ![]() D.
D. ![]()
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����֪{an}�ǵȲ����У�����a1=3��a4=12������{bn}����b1=4��b4=20����{bn��an}Ϊ�ȱ����У�
��1��������{an}��{bn}��ͨ�ʽ��
��2��������{bn}��ǰn��ͣ�
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ��������![]() �ϵĺ���
�ϵĺ���![]() ����
����![]() ����
����![]() ����ƺ���
����ƺ���![]() Ϊ������
Ϊ������![]() �ϵķ��ϸ�����������
�ϵķ��ϸ�����������![]() ����
����![]() ����ƺ���
����ƺ���![]() Ϊ������
Ϊ������![]() �ϵķ��ϸ�����.
�ϵķ��ϸ�����. ![]() .
.
��1��������![]() ������
Ϊ������![]() �ϵķ��ϸ�����������ʵ��
�ϵķ��ϸ�����������ʵ��![]() ��ȡֵ��Χ.
��ȡֵ��Χ.
��2��������![]() ������
Ϊ������![]() �ϵķ��ϸ��������Խⲻ��ʽ
�ϵķ��ϸ��������Խⲻ��ʽ![]() .
.
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����֪��ԲC�� ![]() +
+ ![]() =1��a��b��0����ֱ��y=x+
=1��a��b��0����ֱ��y=x+ ![]() ����ԭ��ΪԲ�ģ�����ԲC�Ķ̰���Ϊ�뾶��Բ���У�F1 �� F2Ϊ�����ҽ��㣬PΪ��ԲC�ϵ�����һ�㣬��F1PF2������ΪG������ΪI����IG��F1F2 ��
����ԭ��ΪԲ�ģ�����ԲC�Ķ̰���Ϊ�뾶��Բ���У�F1 �� F2Ϊ�����ҽ��㣬PΪ��ԲC�ϵ�����һ�㣬��F1PF2������ΪG������ΪI����IG��F1F2 ��
��1������ԲC�ķ��̣�
��2����֪AΪ��ԲC�ϵ��㣬ֱ�ߡҹ��ҽ���F2����ԲC����M��N���㣬��AM��AN��б��k1 �� k2����k1+
k2=�� ![]() ����ֱ��MN�ķ��̣�
����ֱ��MN�ķ��̣�
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ��ij��ɫ�ݿ�ͨ����������������һ���ڵ�ij��ɫ����������![]() ���ݣ�������
���ݣ�������![]() ��Ԫ��֮�������µĶ�Ӧ���ݣ�
��Ԫ��֮�������µĶ�Ӧ���ݣ�
�������� | 2 | 4 | 5 | 6 | 8 |
���� | 30 | 40 | 60 | 50 | 70 |

��1������ɢ��ͼ��
��2����ع�ֱ�߷��̣�
��3���ݴ˹�����������Ϊ12��ʱ������Ϊ����Ԫ��
ע���ٲο���ʽ�����Իع鷽��ϵ����ʽ ��
�� ![]() ��
��
�ڲο����ݣ� ![]() ��
�� ![]() ��
�� ![]() ��
��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ν��������ָ���ǵ���Ϊ�������Σ������ڵ����ϵ���ӰΪ�������������ĵ���������������S��ABC�У�M��SC���е㣬��AM��SB������߳�AB=2 ![]() ����������S��ABC�����Ϊ �� �������ı����Ϊ ��
����������S��ABC�����Ϊ �� �������ı����Ϊ ��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����Բ![]() ���㣺��1����
���㣺��1����![]() �������ҳ�Ϊ2����2����
�������ҳ�Ϊ2����2����![]() ��ֳ�����Բ�����仡���ı�Ϊ
��ֳ�����Բ�����仡���ı�Ϊ![]() .������������1������2��������Բ�У�Բ�ĵ�ֱ��
.������������1������2��������Բ�У�Բ�ĵ�ֱ��![]() �ľ�����С��Բ�ķ���Ϊ__________.
�ľ�����С��Բ�ķ���Ϊ__________.
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����֪������A��BCED������ͼ��ͼ��ʾ�����и���ͼ�Ͳ���ͼ��������Ϊ4�ĵ���ֱ�������Σ�����ͼΪֱ�����Σ� 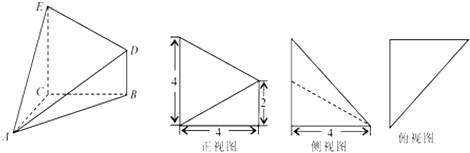
��1����˼���������V�Ĵ�С��
��2��������ֱ��DE��AB���ɽǵ�����ֵ��
��3��������A��ED��B������ֵ��
�鿴�𰸺ͽ���>>
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com