
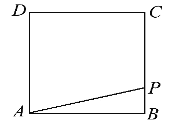
【题目】在边长为4的正方形ABCD的边上有一点P,沿着折线BCDA由点B(起点)向点A(终点)运动.设点P运动的路程为x,△APB的面积为y,且y与x之间的函数关系式用如图所示的程序框图给出.
(1)写出程序框图中①,②,③处应填充的式子.
(2)若输出的面积y值为6,则路程x的值为多少?

 同步练习强化拓展系列答案
同步练习强化拓展系列答案科目:高中数学 来源: 题型:
【题目】在某次测验中,有6位同学的平均成绩为75分.用xn表示编号为n(n=1,2,…,6)的同学所得成绩,且前5位同学同学的成绩如表:
n | 1 | 2 | 3 | 4 | 5 |
x0 | 70 | 76 | 72 | 70 | 72 |
(1)求第6位同学的成绩x6及这6位同学成绩的标准差s;
(2)若从前5位同学中,随机地选2位同学,求恰有1位同学成绩在区间[68,75)中的概率.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】一口袋中装有大小相同的2个白球和4个黑球,每次从袋中任意摸出一个球 .
(1)采取有放回抽样方式,从中摸出两个球,求两球恰好颜色不同的概率;
(2)采取不放回抽样方式,从中摸出两个球,求摸得白球的个数的均值和方差.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图是2017年第一季度五省GDP情况图,则下列陈述中不正确的是( )

A. 2017年第一季度![]() 总量和增速由高到低排位均居同一位的省只有1个
总量和增速由高到低排位均居同一位的省只有1个
B. 与去年同期相比,2017年第一季度五个省的![]() 总量均实现了增长
总量均实现了增长
C. 去年同期河南省的![]() 总量不超过4000亿元
总量不超过4000亿元
D. 2017年第一季度![]() 增速由高到低排位第5的是浙江省
增速由高到低排位第5的是浙江省
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某轮船公司的一艘轮船每小时花费的燃料费与轮船航行速度的平方成正比,比例系数为![]() 轮船的最大速度为15海里
轮船的最大速度为15海里![]() 小时
小时![]() 当船速为10海里
当船速为10海里![]() 小时,它的燃料费是每小时96元,其余航行运作费用(不论速度如何)总计是每小时150元
小时,它的燃料费是每小时96元,其余航行运作费用(不论速度如何)总计是每小时150元![]() 假定运行过程中轮船以速度v匀速航行.
假定运行过程中轮船以速度v匀速航行.
![]() 求k的值;
求k的值;
![]() 求该轮船航行100海里的总费用
求该轮船航行100海里的总费用![]() 燃料费
燃料费![]() 航行运作费用
航行运作费用![]() 的最小值.
的最小值.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com