
【题目】已知y=f(x)是偶函数,定义x≥0时,f(x)=![]()
(1)求f(-2);
(2)当x<-3时,求f(x)的解析式;
(3)设函数y=f(x)在区间[-5,5]上的最大值为g(a),试求g(a)的表达式.
【答案】(1)2; (2)![]() ;(3)
;(3)![]() =
=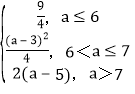 .
.
【解析】
![]() 根据偶函数定义,可得f(-2)=f(2),代入解析式即可求解。
根据偶函数定义,可得f(-2)=f(2),代入解析式即可求解。
![]() 根据偶函数定义,可得f(x)=f(-x),代入即可求得x<-3时的解析式。
根据偶函数定义,可得f(x)=f(-x),代入即可求得x<-3时的解析式。
(3)由偶函数可得函数在[-5,5]上的最大值即为它在区间[0,5]上的最大值;对a分类讨论,讨论在对称轴两侧的单调情况及最值即可。
(1)已知y=f(x)是偶函数,故f(-2)=f(2)=2(3-2)=2;
(2)当x<-3时,f(x)=f(-x)=(-x-3)(a+x)=-(x+3)(a+x),
所以,当x<-3时,f(x)的解析式为f(x)=-(x+3)(a+x)
(3)因为f(x)是偶函数,所以它在区间[-5,5]上的最大值即为它在区间[0,5]上的最大值,
①当a≤3时,f(x)在![]() 上单调递增,在
上单调递增,在![]() 上单调递减,所以
上单调递减,所以![]() ,
,
②当3<a≤7时,f(x)在![]() 与
与![]() 上单调递增,在
上单调递增,在![]() 与
与![]() 上单调递减,
上单调递减,
所以此时只需比较![]() 与
与![]() 的大小.
的大小.
(A)当3<a≤6时,![]() ≥
≥![]() ,所以
,所以![]()
(B)当6<a≤7时,![]() <
<![]() ,所以g(a)=
,所以g(a)=![]()
③当a>7时,f(x)在![]() 与[3,5]上单调递增,在
与[3,5]上单调递增,在![]() 上单调递减,且
上单调递减,且![]() <f(5)=2(a-5),所以g(a)=f(5)=2(a-5),
<f(5)=2(a-5),所以g(a)=f(5)=2(a-5),
综上所述,g(a)=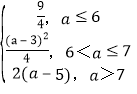


 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案科目:高中数学 来源: 题型:
【题目】如图,四边形ABCD是边长为2的正方形,平面ABCD⊥平面ABEF,AF∥BE,AB⊥BE,AB=BE=2,AF=1.

(Ⅰ)求证:AC⊥平面BDE;
(Ⅱ)求证:AC∥平面DEF;
(Ⅲ)求三棱锥A—DEF的体积.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】有一段演绎推理是这样的: “直线平行于平面,则平行于平面内所有直线;已知直线![]() 平面
平面![]() ,直线
,直线![]() 平面
平面![]() ,直线
,直线![]() ∥平面
∥平面![]() ,则直线
,则直线![]() ∥直线
∥直线![]() ”的结论显然是错误的,这是因为( )
”的结论显然是错误的,这是因为( )
A. 大前提错误 B. 小前提错误 C. 推理形式错误 D. 非以上错误
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】把下列演绎推理写成三段论的形式.
(1)在标准大气压下,水的沸点是100℃,所以在标准大气压下把水加热到100℃时,水会沸腾;
(2)一切奇数都不能被2整除, ![]() 是奇数,所以
是奇数,所以![]() 不能被2整除;
不能被2整除;
(3)三角函数都是周期函数, ![]() 是三角函数,因此
是三角函数,因此![]() 是周期函数.
是周期函数.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】直三棱柱ABC﹣A1B1C1中,∠BCA=90°,M,N分别是A1B1 , A1C1的中点,BC=CA=CC1 , 则BM与AN所成角的余弦值为( )
A.![]()
B.![]()
C.![]()
D.![]()
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】从2017年1月18日开始,支付宝用户可以通过“![]() 扫‘福’字”和“参与蚂蚁森林”两种方式获得福卡(爱国福、富强福、和谐福、友善福、敬业福),除夕夜22:18,每一位提前集齐五福的用户都将获得一份现金红包.某高校一个社团在年后开学后随机调查了80位该校在读大学生,就除夕夜22:18之前是否集齐五福进行了一次调查(若未参与集五福的活动,则也等同于未集齐五福),得到具体数据如下表:
扫‘福’字”和“参与蚂蚁森林”两种方式获得福卡(爱国福、富强福、和谐福、友善福、敬业福),除夕夜22:18,每一位提前集齐五福的用户都将获得一份现金红包.某高校一个社团在年后开学后随机调查了80位该校在读大学生,就除夕夜22:18之前是否集齐五福进行了一次调查(若未参与集五福的活动,则也等同于未集齐五福),得到具体数据如下表:
是否集齐五福 性别 | 是 | 否 | 合计 |
男 | 30 | 10 | 40 |
女 | 35 | 5 | 40 |
合计 | 65 | 15 | 80 |
(1)根据如上的列联表,能否在犯错误的概率不超过0.05的前提下,认为“集齐五福与性别有关”?
(2)计算这80位大学生集齐五福的频率,并据此估算该校10000名在读大学生中集齐五福的人数;
(3)为了解集齐五福的大学生明年是否愿意继续参加集五福活动,该大学的学生会从集齐五福的学生中,选取2位男生和3位女生逐个进行采访,最后再随机选取3次采访记录放到该大学的官方网站上,求最后被选取的3次采访对象中至少有一位男生的概率.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某公司计划购买1台机器,该种机器使用三年后即被淘汰.机器有一易损零件,在购进机器时,可以额外购买这种零件作为备件,每个200元.在机器使用期间,如果备件不足再购买,则每个500元.现需决策在购买机器时应同时购买几个易损零件,为此搜集并整理了100台这种机器在三年使用期内更换的易损零件数,得如图柱状图:
记x表示1台机器在三年使用期内需更换的易损零件数,y表示1台机器在购买易损零件上所需的费用(单位:元),n表示购机的同时购买的易损零件数.
(1)若n=19,求y与x的函数解析式;
(2)若要求“需更换的易损零件数不大于n”的频率不小于0.5,求n的最小值;
(3)假设这100台机器在购机的同时每台都购买19个易损零件,或每台都购买20个易损零件,分别计算这100台机器在购买易损零件上所需费用的平均数,以此作为决策依据,购买1台机器的同时应购买19个还是20个易损零件?
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com