解:(1)∵EO⊥平面ABC,AC?平面ABC
∴EO⊥AC
又∵∠ACB=90°
∴AC⊥BC,BC∩OE=O
∴AC⊥平面BCDE…2分
∵BE?平面BCDE
∴AC⊥BE
∴异直线AC和BE所成角为90°…4分
(2)连接BD,CE,侧面BCDE是菱形,则BD⊥CE
∵AC⊥平面BCDE
∴AC⊥BD
∴BD⊥平面ACE
∴BD⊥AE
过B作BH⊥AE于H,连接DH,则AE⊥平面BHD
∴DH⊥AE,∠BHD为二面角B-AE-D的平面角…6分
设BC=2,则BC=CA=BE=2,AB=2

∵EO⊥BC,BO=CO=1
∴∠EBC=60°,∠BCD=120°
∴BD=2

,CE=2,
在直角△ACE中,得,AE=2

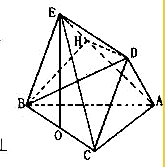
,在△BE中,易得BH=
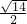
…8分
∴△BHE≌△DHE,
∴DH=BH=
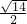
…9分
在△BHD中,由余弦定理得cos∠BHD=-

…11分
即平面ABE与平面ADE所成锐二面角的余弦值为

分析:(1)由已知中∠ACB=90°,EO⊥平面ABC易得EO⊥AC,AC⊥BC,由线面垂直的判定定理可得AC⊥平面BCDE,进而由线面垂直的性质得AC⊥BE,可求异直线AC和BE所成角的大小;
(2)连接BD,CE,由线面垂直的判定定理和性质可得BD⊥AE,过B作BH⊥AE于H,连接DH,可得∠BHD为二面角B-AE-D的平面角,解三角形BDH,即可得到平面ABE与平面ADE所成锐二面角的余弦值.
点评:本题考查的知识点是二面角的平面角及求法,异面直线及其所成的角,其中根据异面直线夹角和二面角的定义,先找出它们的平面角,将问题转化为解三角形问题,是解答此类问题的关键.

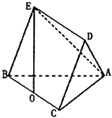 如图,在多面体ABCDE中,底面△ABC为等腰直角三角形,且∠ACB=90°,侧面BCDE是菱形,O点是BC的中点,EO⊥平面ABC.
如图,在多面体ABCDE中,底面△ABC为等腰直角三角形,且∠ACB=90°,侧面BCDE是菱形,O点是BC的中点,EO⊥平面ABC. 解:(1)∵EO⊥平面ABC,AC?平面ABC
解:(1)∵EO⊥平面ABC,AC?平面ABC
 ,CE=2,
,CE=2, ,在△BE中,易得BH=
,在△BE中,易得BH=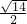 …8分
…8分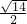 …9分
…9分 …11分
…11分


 如图,在多面体ABC-A1B1C1中,AA1⊥平面ABC,AA1
如图,在多面体ABC-A1B1C1中,AA1⊥平面ABC,AA1 如图,在多面体ABC-A1B1C1中,四边形A1ABB1是正方形,AB=AC,BC=
如图,在多面体ABC-A1B1C1中,四边形A1ABB1是正方形,AB=AC,BC= (2012•青岛二模)如图,在多面体ABC-A1B1C1中,四边形ABB1A1是正方形,AC=AB=1,A1C=A1B,B1C1∥BC,B1C1=
(2012•青岛二模)如图,在多面体ABC-A1B1C1中,四边形ABB1A1是正方形,AC=AB=1,A1C=A1B,B1C1∥BC,B1C1= (2012•合肥一模)如图,在多面体ABC-A1B1C1中,AA1⊥平面ABC,AA1⊥平面ABC,AA1∥=BB1,AB=AC=AA1=
(2012•合肥一模)如图,在多面体ABC-A1B1C1中,AA1⊥平面ABC,AA1⊥平面ABC,AA1∥=BB1,AB=AC=AA1= (2012•郑州二模)如图,在多面体ABC-A1B1C1中,四边形A1ABB1是正方形,AB=AC,BC=
(2012•郑州二模)如图,在多面体ABC-A1B1C1中,四边形A1ABB1是正方形,AB=AC,BC=