
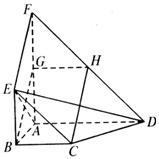
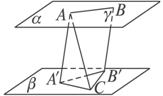
如图,平面ABEF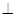 ABCD,四边形ABEF与ABCD都是直角梯形,
ABCD,四边形ABEF与ABCD都是直角梯形,


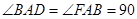 °,BC
°,BC  AD,BE
AD,BE  FA,G、H分别为FA、FD的中点.
FA,G、H分别为FA、FD的中点.
(1)证明四边形BCHG是平行四边行.
(2)C、D、E、F四点是否共面?为什么?
(3)设AB=BE,证明平面ADE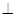 平面CDE.
平面CDE.
(1)证明:由题设知,FG=GA,FH=HD,所以GH 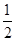 AD.
AD.
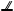
 又BC
又BC 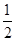 AD,故GH BC.
AD,故GH BC.
 所以四边形BCHG是平行四边形.
所以四边形BCHG是平行四边形.
(2)C、D、F、E四点共面.理由如下:

 由BE
由BE 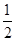 AF,G是FA的中点知,BE GF,所以EF//BG .
AF,G是FA的中点知,BE GF,所以EF//BG .
由(1)知BG//CH,所以EF//CH,故EC、FH共面.
又点D在直线FH上,
所以C、D、F、E四点共面.
(3)证明:连结EG.由AB=BE,BE
AG及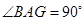 知ABEG是正方形,
知ABEG是正方形,
故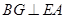 .由题设知,FA、AD、AB两两垂直,故AD
.由题设知,FA、AD、AB两两垂直,故AD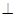 平面FABE,
平面FABE,
因此EA是ED在平面FABE内的射影.根据三垂线定理,BG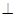 ED.
ED.
又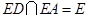 ,所以
,所以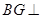 平面ADE.
平面ADE.
由(1)知, CH//BG,所以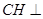 平面ADE.
平面ADE.
由(2)知 平面CDE,故
平面CDE,故 平面CDE,得平面ADE
平面CDE,得平面ADE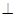 平面CDE.
平面CDE.
【解析】略


 阅读快车系列答案
阅读快车系列答案科目:高中数学 来源: 题型:
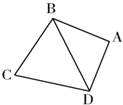 如图平面四边形ABCD中,AB=AD=a,BC=CD=BD 设∠BAD=θ
如图平面四边形ABCD中,AB=AD=a,BC=CD=BD 设∠BAD=θ查看答案和解析>>
科目:高中数学 来源: 题型:
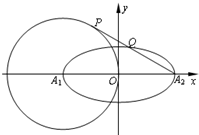 如图平面直角坐标系xOy中,椭圆
如图平面直角坐标系xOy中,椭圆| x2 |
| a2 |
| y2 |
| b2 |
| ||
| 2 |
| PQ |
| QA2 |
查看答案和解析>>
科目:高中数学 来源: 题型:
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com