
【题目】已知函数![]() 为偶函数,且函数
为偶函数,且函数![]() 图象的两相邻对称轴间的距离为
图象的两相邻对称轴间的距离为![]() .
.
(1)求![]() 的值;
的值;
(2)求函数![]() 的对称轴方程;
的对称轴方程;
(3)当![]() 时,方程
时,方程![]() 有两个不同的实根,求m的取值范围。
有两个不同的实根,求m的取值范围。
【答案】(1)![]() .(2)
.(2)![]() ;(3)
;(3) ![]()
【解析】
(1)根据题意求出φ、ω的值,写出f(x)的解析式,计算![]() 的值;(2)由f(x)写出函数
的值;(2)由f(x)写出函数![]() 的解析式,求出对称轴方程;(3)若f(x)=m有两个不同的实根,则函数y=f(x)与y=m有两个不同的交点,令t=2x,
的解析式,求出对称轴方程;(3)若f(x)=m有两个不同的实根,则函数y=f(x)与y=m有两个不同的交点,令t=2x,![]() ,则
,则![]() 的图像与
的图像与![]() 有两个不同交点即可求结果.
有两个不同交点即可求结果.
解:(1)![]() 是偶函数,则φ﹣
是偶函数,则φ﹣![]() =
=![]() +kπ(k∈Z),
+kπ(k∈Z),
解得φ=![]() +kπ(k∈Z),
+kπ(k∈Z),
又因为0<φ<π,所以φ=![]() ,
,
所以![]() =2cosωx;
=2cosωx;
由题意得![]() =2
=2![]() ,所以ω=2;
,所以ω=2;
故f(x)=2cos 2x,
因此![]() =2cos
=2cos ![]() =
=![]() ;
;
(2)由f(x)=2cos 2x,
得![]() =
=![]() ,
,
所以,![]() ,
,
即![]() ,
,
所以函数![]() 的对称轴方程为
的对称轴方程为![]() ;
;
(3)若f(x)=m有两个不同的实根,则函数y=f(x)与y=m有两个不同的交点,函数y=f(x)=2cos 2x,令t=2x,![]() ,则
,则![]() 的图像与
的图像与![]() 有两个不同交点,由图像知
有两个不同交点,由图像知![]()
即m的取值范围是![]() .
.


 阅读快车系列答案
阅读快车系列答案科目:高中数学 来源: 题型:
【题目】已知函数![]() ,
, ![]() .
.
(1)求函数![]() 的最小正周期;
的最小正周期;
(2)若![]() ,且
,且![]() ,求
,求![]() 的值.
的值.
【答案】(1) ![]() (2)
(2) ![]()
【解析】试题分析:(1)根据二倍角公式和两角和差公式得到![]() ,进而得到周期;(2)由
,进而得到周期;(2)由![]() ,得到
,得到![]() ,
, ![]() ,由配凑角公式得到
,由配凑角公式得到![]() ,代入值得到函数值.
,代入值得到函数值.
解析:
(1)由题意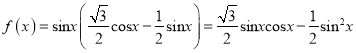
![]() =
=![]()
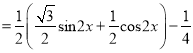
![]()
所以![]() 的最小正周期为
的最小正周期为![]() ;
;
(2)由![]()
![]()
又由![]() 得
得![]() ,所以
,所以![]()
故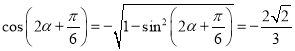 ,
,
故![]()
![]()
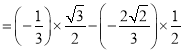
![]()
【题型】解答题
【结束】
20
【题目】为响应十九大报告提出的实施乡村振兴战略,某村庄投资![]() 万元建起了一座绿色农产品加工厂.经营中,第一年支出
万元建起了一座绿色农产品加工厂.经营中,第一年支出![]() 万元,以后每年的支出比上一年增加了
万元,以后每年的支出比上一年增加了![]() 万元,从第一年起每年农场品销售收入为
万元,从第一年起每年农场品销售收入为![]() 万元(前
万元(前![]() 年的纯利润综合=前
年的纯利润综合=前![]() 年的 总收入-前
年的 总收入-前![]() 年的总支出-投资额
年的总支出-投资额![]() 万元).
万元).
(1)该厂从第几年开始盈利?
(2)该厂第几年年平均纯利润达到最大?并求出年平均纯利润的最大值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,抛物线W:y2=4x与圆C:(x-1)2+y2=25交于A,B两点,点P为劣弧![]() 上不同于A,B的一个动点,与x轴平行的直线PQ交抛物线W于点Q,则△PQC的周长的取值范围是( )
上不同于A,B的一个动点,与x轴平行的直线PQ交抛物线W于点Q,则△PQC的周长的取值范围是( )
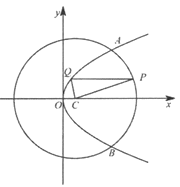
A. (10,14) B. (12,14)
C. (10,12) D. (9,11)
查看答案和解析>>
科目:高中数学 来源: 题型:
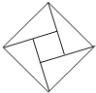
【题目】在北京召开的第24届国际数学家大会会标如图所示,它是由四个相同的直角三角形与中间的小正方形拼成的一个大正方形.若直角三角形中较小的锐角记作![]() ,大正方形的面积是1,小正方形的面积是
,大正方形的面积是1,小正方形的面积是![]() ,则
,则![]() 的值等于( )
的值等于( )
A. 1 B. ![]() C.
C. ![]()
![]() D.
D. ![]()
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】设函数![]() 是定义在
是定义在![]() 上的偶函数,且对任意的
上的偶函数,且对任意的![]() 恒有
恒有![]() ,已知当
,已知当![]() 时,
时,![]() ,则下列命题:
,则下列命题:
①对任意![]() ,都有
,都有![]() ;②函数
;②函数![]() 在
在![]() 上递减,在
上递减,在![]() 上递增;
上递增;
③函数![]() 的最大值是1,最小值是0;④当
的最大值是1,最小值是0;④当![]() 时,
时,![]() .
.
其中正确命题的序号有________.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】设定义在(0,+∞)的单调函数f(x),对任意的x∈(0,+∞)都有f[f(x)﹣log2x]=6.若x0是方程f(x)﹣f′(x)=4的一个解,且 ![]() ,则a=( )
,则a=( )
A.4
B.3
C.2
D.1
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】【2018河北保定市高三上学期期末调研】如图,四面体![]() 中,
中, ![]() 、
、![]() 分别
分别![]() 、
、![]() 的中点,
的中点, ![]() ,
, ![]() .
.
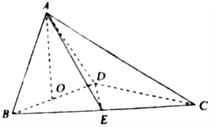
(I)求证: ![]() 平面
平面![]() ;
;
(II)求异面直线![]() 与
与![]() 所成角的余弦值的大小;
所成角的余弦值的大小;
(III)求点![]() 到平面
到平面![]() 的距离.
的距离.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com