
【题目】已知椭圆![]() 的左右焦点分别为
的左右焦点分别为![]() 点.
点.![]() 为椭圆上的一动点,
为椭圆上的一动点,![]() 面积的最大值为
面积的最大值为![]() .过点
.过点![]() 的直线
的直线![]() 被椭圆截得的线段为
被椭圆截得的线段为![]() ,当
,当![]() 轴时,
轴时,![]() .
.
(1)求椭圆![]() 的方程;
的方程;
(2)椭圆![]() 上任取两点A,B,以
上任取两点A,B,以![]() ,
,![]() 为邻边作平行四边形
为邻边作平行四边形![]() .若
.若![]() ,则
,则![]() 是否为定值?若是,求出定值;如不是,请说明理由.
是否为定值?若是,求出定值;如不是,请说明理由.
科目:高中数学 来源: 题型:
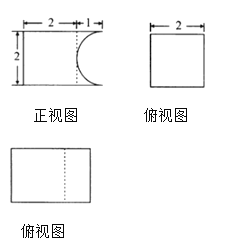
【题目】我国古代科学家祖冲之儿子祖暅在实践的基础上提出了体积计算的原理:“幂势既同,则积不容异”(“幂”是截面积,“势”是几何体的高),意思是两个同高的几何体,如在等高处截面的面积恒相等,则它们的体积相等.已知某不规则几何体与如图所示的三视图所表示的几何体满足“幂势既同”,则该不规则几何体的体积为( )
A. ![]() B.
B. ![]() C.
C. ![]() D.
D. ![]()
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】曲线![]() 为:到两定点
为:到两定点![]() 、
、![]() 距离乘积为常数
距离乘积为常数![]() 的动点
的动点![]() 的轨迹.以下结论正确的个数为( )
的轨迹.以下结论正确的个数为( )
(1)曲线![]() 一定经过原点;
一定经过原点;
(2)曲线![]() 关于
关于![]() 轴、
轴、![]() 轴对称;
轴对称;
(3)![]() 的面积不大于
的面积不大于![]() ;
;
(4)曲线![]() 在一个面积为
在一个面积为![]() 的矩形范围内.
的矩形范围内.
A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某学校积极开展“服务社会,提升自我”的志愿者服务活动,九年级的五名同学(三男两女)成立了“交通秩序维护”小分队.若从该小分队中任选两名同学进行交通秩序维护,则恰是一男一女的概率是________.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】甲、乙两人同时参加一个外贸公司的招聘,招聘分笔试与面试两部分,先笔试后面试.甲笔试与面试通过的概率分别为0.8,0.5,乙笔试与面试通过的概率分别为0.8,0.4,且笔试通过了才能进入面试,面试通过则直接招聘录用,两人笔试与面试相互独立互不影响.
(1)求这两人至少有一人通过笔试的概率;
(2)求这两人笔试都通过却都未被录用的概率;
(3)记这两人中最终被录用的人数为X,求X的分布列和数学期望.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】汽车的“燃油效率”是指汽车每消耗1升汽油行驶的里程,下图描述了甲、乙、丙三辆汽车在不同速度下的燃油效率情况. 下列叙述中正确的是( )

A. 消耗1升汽油,乙车最多可行驶5千米
B. 以相同速度行驶相同路程,三辆车中,甲车消耗汽油最多
C. 甲车以80千米/小时的速度行驶1小时,消耗10升汽油
D. 某城市机动车最高限速80千米/小时. 相同条件下,在该市用丙车比用乙车更省油
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】对于任意![]() ,若数列
,若数列![]() 满足
满足![]() ,则称这个数列为“K数列”.
,则称这个数列为“K数列”.
(1)已知数列:1,![]() ,
,![]() 是“K数列”,求实数m的取值范围;
是“K数列”,求实数m的取值范围;
(2)是否存在首项为-1的无穷等差数列![]() 为“K数列”,且其前n项和
为“K数列”,且其前n项和![]() 满足:
满足:![]() ,若存在,求出
,若存在,求出![]() 的通项公式;若不存在,请说明理由;
的通项公式;若不存在,请说明理由;
(3)已知各项均为正整数的等比数列![]() (至少有4项)为“K数列”,数列
(至少有4项)为“K数列”,数列![]() 不是“K数列”,若
不是“K数列”,若![]() ,是否存在
,是否存在![]() ,使
,使![]() 为“K数列”?若存在,请求出,
为“K数列”?若存在,请求出,![]() 若不存在,请说明理由.
若不存在,请说明理由.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com