
【题目】若存在实常数![]() 和
和![]() ,使得函数
,使得函数![]() 和
和![]() 对其公共定义域上的任意实数
对其公共定义域上的任意实数![]() 都满足:
都满足:![]() 和
和![]() 恒成立,则称此直线
恒成立,则称此直线![]() 为
为![]() 和
和![]() 的“隔离直线”,已知函数
的“隔离直线”,已知函数![]() ,
,![]() ,
,![]() ,下列命题为真命题的是( )
,下列命题为真命题的是( )
A.![]() 在
在![]() 内单调递减
内单调递减
B.![]() 和
和![]() 之间存在“隔离直线”,且
之间存在“隔离直线”,且![]() 的最小值为
的最小值为![]()
C.![]() 和
和![]() 之间存在“隔离直线”,且
之间存在“隔离直线”,且![]() 的取值范围是
的取值范围是![]()
D.![]() 和
和![]() 之间存在唯一的“隔离直线”
之间存在唯一的“隔离直线”![]()
科目:高中数学 来源: 题型:
【题目】将边长为3的正![]() 的各边三等分,过每个分点分别作另外两边的平行线,称
的各边三等分,过每个分点分别作另外两边的平行线,称![]() 的边及这些平行线所交的10个点为格点.若在这10个格点中任取
的边及这些平行线所交的10个点为格点.若在这10个格点中任取![]() 个格点,一定存在三个格点能构成一个等腰三角形(包括正三角形).求
个格点,一定存在三个格点能构成一个等腰三角形(包括正三角形).求![]() 的最小值.
的最小值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】今年消毒液和口罩成了抢手年货,老百姓几乎人人都需要,但对于![]() 这种口罩,大多数人不是很了解.现随机抽取40人进行调查,其中45岁以下的有20人,在接受调查的40人中,对于
这种口罩,大多数人不是很了解.现随机抽取40人进行调查,其中45岁以下的有20人,在接受调查的40人中,对于![]() 这种口罩了解的占
这种口罩了解的占![]() ,其中45岁以上(含45岁)的人数占
,其中45岁以上(含45岁)的人数占![]() .
.
(1)将答题卡上的列联表补充完整;
(2)判断是否有![]() 的把握认为对
的把握认为对![]() 这种口罩的了解与否与年龄有关.
这种口罩的了解与否与年龄有关.
参考公式: ,其中
,其中![]() .
.
参考数据:
|
|
|
|
|
|
|
|
|
|
查看答案和解析>>
科目:高中数学 来源: 题型:
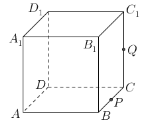
【题目】如图,正方体![]() 的棱长为1,
的棱长为1,![]() 为
为![]() 的中点,
的中点,![]() 为线段
为线段![]() 上的动点,过点
上的动点,过点![]()
![]()
![]() 的平面截该正方体所得的截面记为
的平面截该正方体所得的截面记为![]() ,给出下列三个结论:
,给出下列三个结论:
① 当![]() 时,
时,![]() 为四边形;
为四边形;
② 当![]() 时,
时,![]() 为等腰梯形;
为等腰梯形;
③ 当![]() 时,
时,![]() 的面积为
的面积为![]() ;
;
以上结论正确的个数是( )
A.0B.1C.2D.3
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数f(x)=(m2-m-1)x-5m-3,m为何值时,f(x):
(1)是幂函数;
(2)是正比例函数;
(3)是反比例函数;
(4)是二次函数.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在非负数构成的![]() 数表
数表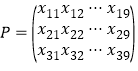 中,每行的数互不相同,前六列中每列的三数之和为1,
中,每行的数互不相同,前六列中每列的三数之和为1,![]() 均大于1.如果
均大于1.如果![]() 的前三列构成的数表
的前三列构成的数表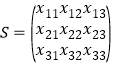 满足下面的性质
满足下面的性质![]() :对于数表
:对于数表![]() 中的任意一列
中的任意一列![]() (
(![]() )均存在某个
)均存在某个![]() 使得
使得![]() .①
.①
求证:(1)最小值![]() (
(![]() )一定去自数表
)一定去自数表![]() 的不同列;
的不同列;
(2)存在数表![]() 中唯一的一列
中唯一的一列![]() (
(![]() )使得
)使得![]() 数表
数表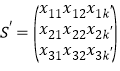 仍然具有性质(
仍然具有性质(![]() ).
).
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知数列{an}的通项公式为an=n2-n-30.
(1)求数列的前三项,60是此数列的第几项?
(2)n为何值时,an=0,an>0,an<0?
(3)该数列前n项和Sn是否存在最值?说明理由.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com