
【题目】已知函数![]() .
.
(1)当x∈[1,4]时,求函数![]() 的值域;
的值域;
(2)如果对任意的x∈[1,4],不等式![]() 恒成立,求实数k的取值范围
恒成立,求实数k的取值范围
【答案】(1) [0,2]. (2) (-∞,-3).
【解析】
试题分析:(1) 令t=log2x,则函数h(x)转化为关于t 的二次函数:h(x)=-2(t-1)2+2 ,根据x∈[1,4],得t∈[0,2],结合对称轴与定义区间位置关系确定函数最值和值域(2) 令t=log2x,则(3-4t)(3-t)>k·t对一切t∈[0,2]恒成立,当t=0时,k∈R;当t∈(0,2]时,利用变量分离法转化为对应函数最值:![]() 最小值,根据基本不等式求最值:
最小值,根据基本不等式求最值:![]() 即得实数k的取值范围
即得实数k的取值范围
试题解析:(1)h(x)=(4-2log2x)·log2x=-2(log2x-1)2+2,
因为x∈[1,4],所以log2x∈[0,2],
故函数h(x)的值域为[0,2].
(2)由f(x2)·f()>k·g(x),
得(3-4log2x)(3-log2x)>k·log2x,
令t=log2x,因为x∈[1,4],所以t=log2x∈[0,2],
所以(3-4t)(3-t)>k·t对一切t∈[0,2]恒成立,
①当t=0时,k∈R;
②当t∈(0,2]时,![]() 恒成立,即
恒成立,即![]() ,因为
,因为![]() ,当且仅当
,当且仅当![]() 即
即![]() 时取等号,所以
时取等号,所以![]() 的最小值为-3,
的最小值为-3,
综上,k∈(-∞,-3).


 阅读快车系列答案
阅读快车系列答案科目:高中数学 来源: 题型:
【题目】已知正方形![]() 的边长为1,弧
的边长为1,弧![]() 是以点
是以点![]() 为圆心的圆弧.
为圆心的圆弧.

(1)在正方形内任取一点![]() ,求事件“
,求事件“![]() ”的概率;
”的概率;
(2)用大豆将正方形均匀铺满,经清点,发现大豆一共28粒,其中有22粒落在圆中阴影部分内,请据此估计圆周率![]() 的近似值(精确到
的近似值(精确到![]() ).
).
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】选修4-4:坐标系与参数方程
在直角坐标系![]() 中,直线
中,直线![]() 的方程是
的方程是![]() ,圆
,圆![]() 的参数方程是
的参数方程是![]() (
(![]() 为参数).以原点
为参数).以原点![]() 为极点,
为极点,![]() 轴的非负半轴为极轴建立极坐标系.
轴的非负半轴为极轴建立极坐标系.
(1)分别求直线![]() 与圆
与圆![]() 的极坐标方程;
的极坐标方程;
(2)射线![]() :
:![]() (
(![]() )与圆
)与圆![]() 的交点为
的交点为![]() 、
、![]() 两点,与直线
两点,与直线![]() 交于点
交于点![]() ,射线
,射线![]() :
:![]() 与圆
与圆![]() 交于
交于![]() ,
,![]() 两点,与直线
两点,与直线![]() 交于点
交于点![]() ,求
,求![]() 的最大值.
的最大值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】甲、乙两人玩数字游戏,先由甲任想一个数字记为![]() ,再由乙猜甲刚才想的数字把乙想的数字记为
,再由乙猜甲刚才想的数字把乙想的数字记为![]() ,且
,且![]() ,
, ![]() ,记
,记![]() .
.
(1)求![]() 的概率;
的概率;
(2)若![]() ,则称“甲乙心有灵犀”,求“甲乙心有灵犀”的概率.
,则称“甲乙心有灵犀”,求“甲乙心有灵犀”的概率.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某商品进货价每件50元,据市场调查,当销售价格(每件x元)在50≤ x ≤80时,每天售出的件数为P=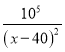 ,每天获得的利润为y(元)
,每天获得的利润为y(元)
(1)写出关于x的函数y的表达式;
(2)若想每天获得的利润最多,问售价应定为每件多少元?
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】设关于![]() 的一元二次方程
的一元二次方程![]() .
.
(1)若![]() 是从0,1,2,3四个数中任取的一个数,
是从0,1,2,3四个数中任取的一个数,![]() 是从0,1,2三个数中任取的一个数,求上述方程有实根的概率;
是从0,1,2三个数中任取的一个数,求上述方程有实根的概率;
(2)若![]() 是从区间
是从区间![]() 任取的一个数,
任取的一个数,![]() 是从区间
是从区间![]() 任取的一个数,求上述方程有根的概率.
任取的一个数,求上述方程有根的概率.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com