已知正数等差数列{an}的前n项和为Sn,S12=24,则a6-a7最大值为( )
A.36
B.6
C.4
D.2
【答案】
分析:由正数等差数列{a
n}的前n项和为S
n,S
12=24,知a
6+a
7=4,由数列{a
n}是正数等差数列,a
6-a
7最大值要小于4,由此能求出结果.
解答:解:∵正数等差数列{a
n}的前n项和为S
n,S
12=24,
∴
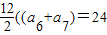
,
∴a
6+a
7=4,
∵数列{a
n}是正数等差数列,
∴a
6-a
7最大值要小于4,
故选D.
点评:本题考查等差数列的通项公式和前n项和公式的应用,是基础题.解题时要认真审题,仔细解答.

 阅读快车系列答案
阅读快车系列答案