
【题目】在如图所示的三棱锥![]() 中,
中,![]() 分别是
分别是![]() 的中点.
的中点.
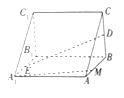
(1)求证:![]() 平面
平面![]() ;
;
(2)若![]() 为正三角形,且
为正三角形,且![]() 为
为![]() 上的一点,
上的一点,![]() ,求直线
,求直线![]() 与直线
与直线![]() 所成角的正切值.
所成角的正切值.
 黄冈小状元解决问题天天练系列答案
黄冈小状元解决问题天天练系列答案科目:高中数学 来源: 题型:
【题目】已知圆C:x2+y2=9,点A(-5,0),直线l:x-2y=0.
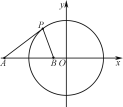
(1)求与圆C相切,且与直线l垂直的直线方程;
(2)在直线OA上(O为坐标原点),存在定点B(不同于点A),满足:对于圆C上任一点P,都有![]() 为一常数,试求所有满足条件的点B的坐标.
为一常数,试求所有满足条件的点B的坐标.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数![]() .
.
(1)求函数![]() 的极值;
的极值;
(2)对于曲线上的不同两点![]() ,如果存在曲线上的点
,如果存在曲线上的点![]() ,且
,且![]() 使得曲线在点
使得曲线在点![]() 处的切线
处的切线![]() ,则称
,则称![]() 为弦
为弦![]() 的伴随直线,特别地,当
的伴随直线,特别地,当![]() 时,又称
时,又称![]() 为
为![]() 的
的![]() —伴随直线.
—伴随直线.
①求证:曲线![]() 的任意一条弦均有伴随直线,并且伴随直线是唯一的;
的任意一条弦均有伴随直线,并且伴随直线是唯一的;
②是否存在曲线![]() ,使得曲线
,使得曲线![]() 的任意一条弦均有
的任意一条弦均有![]() —伴随直线?若存在,给出一条这样的曲线,并证明你的结论;若不存在,说明理由.
—伴随直线?若存在,给出一条这样的曲线,并证明你的结论;若不存在,说明理由.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某校高一(1)班有男同学45名,女同学15名,老师按照分层抽样的方法抽取4人组建了一个课外兴趣小组.
(I)求课外兴趣小组中男、女同学的人数;
(II)经过一个月的学习、讨论,这个兴趣小组决定选出两名同学做某项实验,方法是从小组里选出一名同学做实验,该同学做完后,再从小组内剩下的同学中选出一名同学做实验,求选出的两名同学中恰有一名女同学的概率;
(III)在(II)的条件下,第一次做实验的同学A得到的实验数据为38,40,41,42,44,第二次做实验的同学B得到的实验数据为39,40,40,42,44,请问哪位同学的实验更稳定?并说明理由.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某大学开设甲、乙、丙三门选修课,学生是否选修哪门课互不影响,已知某学生只选修甲的概率为0.08,只选修甲和乙的概率是0.12,至少选修一门的概率是0.88,用![]() 表示该学生选修的课程门数和没有选修的课程门数的乘积.
表示该学生选修的课程门数和没有选修的课程门数的乘积.
(1)记“函数![]() 为
为![]() 上的偶函数”为事件
上的偶函数”为事件![]() ,求事件
,求事件![]() 的概率;
的概率;
(2)求![]() 的分布列和数学期望.
的分布列和数学期望.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知二次函数f(x)满足f(x+1)-f(x)=-2x+1,且f(2)=15.
(1)求函数f(x)的解析式;
(2) 令g(x)=(2-2m)x-f(x).
① 若函数g(x)在x∈[0,2]上是单调函数,求实数m的取值范围;
② 求函数g(x)在x∈[0,2]上的最小值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知椭圆![]()
![]()
![]() 的离心率为
的离心率为![]() ,短轴一个端点到右焦点的距离为
,短轴一个端点到右焦点的距离为![]() .
.
(1) 求椭圆![]() 的方程;
的方程;
(2) 设直线![]() 与椭圆
与椭圆![]() 交于
交于![]() 、
、![]() 两点,坐标原点
两点,坐标原点![]() 到直线
到直线![]() 的距离为
的距离为![]() ,求
,求![]() 面积的最大值.
面积的最大值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】(本小题满分12分)已知![]() 是定义在
是定义在![]() 上的奇函数,且
上的奇函数,且![]() ,当
,当![]()
![]() ,
,![]() 时,有
时,有![]() 成立.
成立.
(Ⅰ)判断![]() 在
在![]() 上的单调性,并加以证明;
上的单调性,并加以证明;
(Ⅱ)若![]() 对所有的
对所有的![]() 恒成立,求实数m的取值范围.
恒成立,求实数m的取值范围.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com