
【题目】已知函数![]()
(1)讨论![]() 的奇偶性,并说明理由;
的奇偶性,并说明理由;
(2)若![]() 对任意实数
对任意实数![]() 恒成立,求实数
恒成立,求实数![]() 的取值范围;
的取值范围;
(3)若![]() 在
在![]() 上有最大值9,求
上有最大值9,求![]() 的值.
的值.
【答案】(1) 当![]() 时,为偶函数;当
时,为偶函数;当![]() 时,为非奇非偶函数;(2)
时,为非奇非偶函数;(2) ![]() 或
或![]() ;(3)
;(3) ![]() 或
或![]() 。
。
【解析】
(1)通过a的值是否为0,利用奇偶性的定义,直接判断f(x)的奇偶性;
(2)通过a=16,利用函数的单调性的定义判断f(x)在x∈(0,2]上的单调性即可;
(3)利用二次函数对称轴与区间的关系的讨论,分别求解最大值,再进行取舍.
(1)当![]() 时,为偶函数;当
时,为偶函数;当![]() 时,为非奇非偶函数;
时,为非奇非偶函数;
当![]() 时,
时,![]() ,满足f(-x)=f(x),所以为偶函数;
,满足f(-x)=f(x),所以为偶函数;
当![]() 时,
时,![]() ,即
,即![]() ,
,
同样![]() ,所以为非奇非偶函数;
,所以为非奇非偶函数;
(2)![]() >2对任意实数
>2对任意实数![]() 恒成立,即
恒成立,即![]() 对任意实数
对任意实数![]() 恒成立,所以只需
恒成立,所以只需![]() ,解得
,解得![]() 或
或![]() ;
;
(3)![]() ,对称轴为
,对称轴为![]()
①当![]() ,即
,即![]() 时,
时,![]() ,
,
解得![]() 或
或![]() (舍去)
(舍去)
②当![]() ,即
,即![]() 时,
时,![]() ,解得
,解得![]() 或
或![]() (舍去)
(舍去)
综上:![]() 或
或![]() .
.


 云南师大附小一线名师提优作业系列答案
云南师大附小一线名师提优作业系列答案 冲刺100分单元优化练考卷系列答案
冲刺100分单元优化练考卷系列答案科目:高中数学 来源: 题型:
【题目】![]() 总决赛采用7场4胜制,2018年总决赛两支球队分别为勇士和骑士,假设每场比赛勇士获胜的概率为0.7,骑士获胜的概率为0.3,且每场比赛的结果相互独立,则恰好5场比赛决出总冠军的概率为__________.
总决赛采用7场4胜制,2018年总决赛两支球队分别为勇士和骑士,假设每场比赛勇士获胜的概率为0.7,骑士获胜的概率为0.3,且每场比赛的结果相互独立,则恰好5场比赛决出总冠军的概率为__________.
查看答案和解析>>
科目:高中数学 来源: 题型:
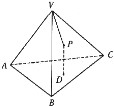
【题目】如图,P是正四面体V-ABC的面VBC上一点,点P到平面ABC距离与到点V的距离相等,则动点P的轨迹是( )
A. 直线 B. 抛物线
C. 离心率为![]() 的椭圆 D. 离心率为3的双曲线
的椭圆 D. 离心率为3的双曲线
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在如图所示的几何体中,四边形ABCD是等腰梯形,AB∥CD,∠DAB=60°,FC⊥平面ABCD,AE⊥BD,CB=CD=CF. 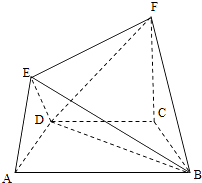
(1)求证:BD⊥平面AED;
(2)求二面角F﹣BD﹣C的余弦值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】“中国人均读书![]() 本(包括网络文学和教科书),比韩国的
本(包括网络文学和教科书),比韩国的![]() 本、法国的
本、法国的![]() 本、日本的
本、日本的![]() 本、犹太人的
本、犹太人的![]() 本少得多,是世界上人均读书最少的国家”,这个论断被各种媒体反复引用.出现这样统计结果无疑是令人尴尬的,而且和其他国家相比,我国国民的阅读量如此之低,也和我国是传统的文明古国、礼仪之邦的地位不相符.某小区为了提高小区内人员的读书兴趣,特举办读书活动,准备进一定量的书籍丰富小区图书站,由于不同年龄段需看不同类型的书籍,为了合理配备资源,现对小区内看书人员进行年龄调查,随机抽取了一天
本少得多,是世界上人均读书最少的国家”,这个论断被各种媒体反复引用.出现这样统计结果无疑是令人尴尬的,而且和其他国家相比,我国国民的阅读量如此之低,也和我国是传统的文明古国、礼仪之邦的地位不相符.某小区为了提高小区内人员的读书兴趣,特举办读书活动,准备进一定量的书籍丰富小区图书站,由于不同年龄段需看不同类型的书籍,为了合理配备资源,现对小区内看书人员进行年龄调查,随机抽取了一天![]() 名读书者进行调查,将他们的年龄分成
名读书者进行调查,将他们的年龄分成![]() 段:
段:![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() 后得到如图所示的频率分布直方图.问:
后得到如图所示的频率分布直方图.问:

(1)估计在这![]() 名读书者中年龄分布在
名读书者中年龄分布在![]() 的人数;
的人数;
(2)求这![]() 名读书者年龄的平均数和中位数;
名读书者年龄的平均数和中位数;
(3)若从年龄在![]() 的读书者中任取
的读书者中任取![]() 名,求这两名读书者年龄在
名,求这两名读书者年龄在![]() 的人数恰为
的人数恰为![]() 的概率.
的概率.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】(1)若函数f(x)=ax2-x-1有且仅有一个零点, 求实数a的值.
(2)若函数f(x)=|4x-x2|+a有4个零点,求实数a的取值范围.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com