【题目】抛物线
的焦点为F ，已知点A ，B 为抛物线上的两个动点，且满足
.过弦AB 的中点M 作抛物线准线的垂线MN ，垂足为N，则
的最大值为__________．
【答案】1
【解析】
设|AF|=a，|BF|=b，连接AF、BF．由抛物线定义得2|MN|=a+b，由余弦定理可得|AB|2=
（a+b）2﹣3ab，进而根据基本不等式，求得|AB|的取值范围，从而得到本题答案．
设|AF|=a，|BF|=b，
由抛物线定义，得AF|=|AQ|，|BF|=|BP|
在梯形ABPQ中，∴2|MN|=|AQ|+|BP|=a+b．
由余弦定理得，
|AB|2=a2+b2﹣2abcos60°=a2+b2﹣ab
配方得，|AB|2=（a+b）2﹣3ab，
又∵ab≤（
） 2，
∴（a+b）2﹣3ab≥（a+b）2﹣
（a+b）2=
（a+b）2
得到|AB|≥
（a+b）．
∴
≤1，即的最大值为1．
故答案为：1．
科目：高中数学 来源： 题型：
【题目】已知椭圆
的标准方程为
，该椭圆经过点
，且离心率为
．
（1）求椭圆的标准方程；
（2）过椭圆长轴上一点
作两条互相垂直的弦
．若弦的中点分别为
，证明：直线
恒过定点．
查看答案和解析>>
科目：高中数学 来源： 题型：
【题目】在平面直角坐标系xOy中，已知椭圆C：
(a＞b＞0)过点
，离心率为
.
（1）求椭圆C的方程；
（2）若斜率为
的直线l与椭圆C交于A，B两点，试探究
是否为定值？若是定值，则求出此定值；若不是定值，请说明理由．
查看答案和解析>>
科目：高中数学 来源： 题型：
【题目】命题
方程
表示双曲线；命题
不等式
的解集是
. 
为假， 
为真，求
的取值范围.
【答案】
【解析】试题分析：由命题
方程
表示双曲线，求出
的取值范围，由命题
不等式
的解集是
，求出
的取值范围，由
为假， 
为真，得出
一真一假，分两种情况即可得出
的取值范围.
试题解析：
真 
，
真 
或
∴
真
假 
假
真 
∴
范围为
【题型】解答题
【结束】
18
【题目】如图，设
是圆
上的动点，点
是
在
轴上的投影， 
为
上一点，且
.
（1）当
在圆上运动时，求点
的轨迹
的方程；
（2）求过点
且斜率为
的直线被
所截线段的长度.
查看答案和解析>>
科目：高中数学 来源： 题型：
【题目】已知直线l的参数方程为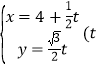
为参数
，以坐标原点为极点，x轴的正半轴为极轴建建立极坐标系，曲线C的极坐标方程为
．
求曲线C的直角坐标方程与直线l的极坐标方程；
Ⅱ若直线
与曲线C交于点
不同于原点，与直线l交于点B，求
的值．
查看答案和解析>>
科目：高中数学 来源： 题型：
【题目】某工艺公司要对某种工艺品深加工，已知每个工艺品进价为20元，每个的加工费为n元，销售单价为x元.根据市场调查，须有
，
，
，同时日销售量m（单位：个）与
成正比.当每个工艺品的销售单价为29元时，日销售量为1000个.
（1）写出日销售利润y（单位：元）与x的函数关系式；
（2）当每个工艺品的加工费用为5元时，要使该公司的日销售利润为100万元，试确定销售单价x的值.（提示：函数
与
的图象在
上有且只有一个公共点）
查看答案和解析>>
科目：高中数学 来源： 题型：
【题目】先阅读下列不等式的证法，再解决后面的问题：
已知
，
，求证：
.
证明：构造函数
，
即
.
因为对一切
，恒有
，
所以
，从而得.
（1）若
，
，请写出上述结论的推广式；
（2）参考上述证法，对你推广的结论加以证明.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com
