
【题目】已知函数f(x)= ![]() ,若方程f(x)=a有四个不同的解x1 , x2 , x3 , x4 , 且x1<x2<x3<x4 , 则x3(x1+x2)+
,若方程f(x)=a有四个不同的解x1 , x2 , x3 , x4 , 且x1<x2<x3<x4 , 则x3(x1+x2)+ ![]() 的取值范围是( )
的取值范围是( )
A.(﹣1,+∞)
B.(﹣1,1]
C.(﹣∞,1)
D.[﹣1,1)
科目:高中数学 来源: 题型:
【题目】给出下列五个命题: ①函数 ![]() 的一条对称轴是x=
的一条对称轴是x= ![]() ;
;
②函数y=tanx的图象关于点( ![]() ,0)对称;
,0)对称;
③正弦函数在第一象限为增函数;
④若 ![]() ,则x1﹣x2=kπ,其中k∈Z;
,则x1﹣x2=kπ,其中k∈Z;
⑤函数f(x)=sinx+2|sinx|,x∈[0,2π]的图象与直线y=k有且仅有两个不同的交点,则k的取值范围为(1,3).
以上五个命题中正确的有(填写所有正确命题的序号)
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,四棱锥P—ABCD中,PD![]() 底面ABCD,AB//DC,AD
底面ABCD,AB//DC,AD![]() DC,AB=AD=1,DC=2,PD=
DC,AB=AD=1,DC=2,PD=![]() ,M为棱PB的中点.
,M为棱PB的中点.
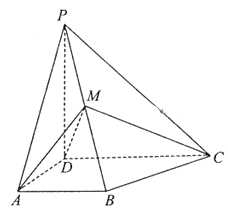
(1)证明:DM![]() 平面PBC;
平面PBC;
(2)求二面角A—DM—C的余弦值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数![]() ,其中
,其中![]() 为常数.
为常数.
(1)当![]() ,且
,且![]() 时,判断函数
时,判断函数![]() 是否存在极值,若存在,求出极值点;若不存在,说明理由;
是否存在极值,若存在,求出极值点;若不存在,说明理由;
(2)若![]() ,对任意的正整数
,对任意的正整数![]() ,当
,当![]() 时,求证:
时,求证:![]() .
.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知椭圆 ![]() =1(a>b>0)的离心率为
=1(a>b>0)的离心率为 ![]() ,坐标原点O到过点A(0,﹣b)和B(a,0)的直线的距离为
,坐标原点O到过点A(0,﹣b)和B(a,0)的直线的距离为 ![]() .又直线y=kx+m(k≠0,m≠0)与该椭圆交于不同的两点C,D.且C,D两点都在以A为圆心的同一个圆上.
.又直线y=kx+m(k≠0,m≠0)与该椭圆交于不同的两点C,D.且C,D两点都在以A为圆心的同一个圆上.
(1)求椭圆的方程;
(2)求△ABC面积的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知圆O的方程为x2+y2=4,P是圆O上的一个动点,若线段OP的垂直平分线总是被平面区域|x|+|y|≥a覆盖,则实数a的取值范围是( )
A.0≤a≤2
B.![]()
C.0≤a≤1
D.a≤1
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】下列函数中,奇函数的个数为( ) ①y=x2sinx ②y=sinx , x∈ ![]() ③y=xcosx , x∈
③y=xcosx , x∈ ![]() ④y=tanx .
④y=tanx .
A.1个
B.2个
C.3个
D.4个
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】设数列{an}的前n项和为Sn , 若对于任意的n∈N* , 都有Sn=2an﹣3n.
(1)求证{an+3}是等比数列
(2)求数列{an}的通项公式;
(3)求数列{an}的前n项和Sn .
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com