解:(1)∵

=(sinA+sinC,sinB-sinA),

=(sinA-sinC,sinB),且

⊥

,
∴

•

=(sinA+sinC)(sinA-sinC)+sinB(sinB-sinA)=0,
即sin
2A-sin
2C+sin
2B-sinAsinB=0,
整理得:sin
2C=sin
2A+sin
2B-sinAsinB,
由正弦定理得:c
2=a
2+b
2-ab,即a
2+b
2-c
2=ab,
再由余弦定理得:cosC=

=

,
∵0<C<π,∴C=

;
(2)∵a
2=b
2+

c
2,
∴sin
2A=sin
2B+

sin
2C,即sin
2A-sin
2B=

,
∴
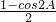
-
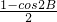
=

,即cos2B-cos2A=

,
∵A+B+C=π,即A+B=

,
∴cos(

-2A)-cos2A=

,即-cos(

-2A)-cos2A=

,
整理得:

cos2A+

sin2A+cos2A=-

,即

cos2A+

sin2A=-

,
∴sin(2A+

)=-

,
则sin(A-B)=sin[A-(

-A)]=sin(2A-

)=-sin(2A-

+π)=-sin(2A+

)=

.
分析:(1)由两向量的坐标,及两向量垂直,得到其数量积为0,根据平面向量的数量积运算法则化简,整理后再利用正弦定理化简,利用余弦定理表示出cosC,将得出的关系式变形后代入求出cosC的值,由C为三角形的内角,利用特殊角的三角函数值即可求出C的度数;
(2)利用正弦定理化简已知的等式,将C的度数代入,并利用二倍角的余弦函数公式化简后,再由三角形的内角和定理及C的度数,用A表示出B,代入化简后的式子中,利用两角和与差的余弦函数公式及特殊角的三角函数值化简,整理后再利用两角和与差的正弦函数公式化简求出sin(2A+

)的值,然后将表示出的B代入所求的式子中,整理后利用诱导公式化简,将求出的sin(2A+

)的值代入即可求出所求式子的值.
点评:此题考查了正弦、余弦定理,平面向量的数量积运算法则,二倍角的余弦函数公式,诱导公式,两角和与差的正弦、余弦函数公式,以及特殊角的三角函数值,熟练掌握定理及公式是解本题的关键.

 =(sinA+sinC,sinB-sinA),
=(sinA+sinC,sinB-sinA), =(sinA-sinC,sinB),且
=(sinA-sinC,sinB),且 ,
,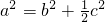 ,试求sin(A-B)的值.
,试求sin(A-B)的值. =(sinA+sinC,sinB-sinA),
=(sinA+sinC,sinB-sinA), =(sinA-sinC,sinB),且
=(sinA-sinC,sinB),且 ⊥
⊥ ,
, •
• =(sinA+sinC)(sinA-sinC)+sinB(sinB-sinA)=0,
=(sinA+sinC)(sinA-sinC)+sinB(sinB-sinA)=0, =
= ,
, ;
; c2,
c2, sin2C,即sin2A-sin2B=
sin2C,即sin2A-sin2B= ,
,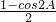 -
-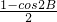 =
= ,即cos2B-cos2A=
,即cos2B-cos2A= ,
, ,
, -2A)-cos2A=
-2A)-cos2A= ,即-cos(
,即-cos( -2A)-cos2A=
-2A)-cos2A= ,
, cos2A+
cos2A+ sin2A+cos2A=-
sin2A+cos2A=- ,即
,即 cos2A+
cos2A+ sin2A=-
sin2A=- ,
, )=-
)=- ,
, -A)]=sin(2A-
-A)]=sin(2A- )=-sin(2A-
)=-sin(2A- +π)=-sin(2A+
+π)=-sin(2A+ )=
)= .
. )的值,然后将表示出的B代入所求的式子中,整理后利用诱导公式化简,将求出的sin(2A+
)的值,然后将表示出的B代入所求的式子中,整理后利用诱导公式化简,将求出的sin(2A+ )的值代入即可求出所求式子的值.
)的值代入即可求出所求式子的值.

 每日10分钟口算心算速算天天练系列答案
每日10分钟口算心算速算天天练系列答案