
 ,求红球的个数.
,求红球的个数. 建立等式关系,求出n的值,从而求出红球的个数.
建立等式关系,求出n的值,从而求出红球的个数.
 ,P(ξ=3)=
,P(ξ=3)=
 ,P(ξ=5)=
,P(ξ=5)= ,P(ξ=6)=
,P(ξ=6)=
| ξ | 2 | 3 | 4 | 5 | 6 |
| P |  |  |  |  |  |
 +3×
+3× +4×
+4× +5×
+5× +6×
+6× =
=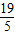
 解得0<ξ<4即ξ=2,3
解得0<ξ<4即ξ=2,3


科目:高中数学 来源: 题型:
| 2 |
| 5 |
| 7 |
| 9 |
查看答案和解析>>
科目:高中数学 来源: 题型:
| 4 | 15 |
查看答案和解析>>
科目:高中数学 来源: 题型:
(本小题满分12分)袋中装有10个大小相同的小球,其中黑球3个,白球n个(![]() ,其余均为红球;
,其余均为红球;
(1):从袋中一次任取2个球,如果这2个球颜色相同的概率是![]() ,求红球的个数。
,求红球的个数。
(2):在(1)的条件下,从袋中任取2个球,若取一个白球记1分,取一个黑球记2分,取一个红球记3分,用![]() 表示取出的两个球的得分的和;
表示取出的两个球的得分的和;
①求随机变量![]() 的分布列及期望
的分布列及期望![]() 。w.w.^w.k.&s.5*u.c.#om
。w.w.^w.k.&s.5*u.c.#om
②记“关于x的不等式![]() 的解集是实数集R”为事件A,求事件A发生的概率。
的解集是实数集R”为事件A,求事件A发生的概率。
查看答案和解析>>
科目:高中数学 来源:2014届天津市高三第一次六校联考理科数学试卷(解析版) 题型:解答题
一个袋中装有10个大小相同的小球.其中白球5个、黑球4个、红球1个.
(1)从袋中任意摸出2个球,求至少得到1个白球的概率;
(2)从袋中任意摸出3个球,记得到白球的个数为 ,求随机变量
,求随机变量 的数学期望
的数学期望 .
.
查看答案和解析>>
科目:高中数学 来源: 题型:
(本小题满分14分)
袋中装有10个大小相同的小球,其中黑球3个,白球![]() 个,其余均为红球;
个,其余均为红球;
(1)从袋中一次任取2个球,如果这2个球颜色相同的概率是![]() ,求红球的个数.
,求红球的个数.
(2)在(1)的条件下,从袋中任取2个球,若取一个白球记1分,取一个黑球记2分,取一个红球记3分,用![]() 表示取出的两个球的得分的和;
表示取出的两个球的得分的和;
①求随机变量![]() 的分布列及期望
的分布列及期望![]() .^
.^
②记“关于x的不等式![]() 的解集是实数集
的解集是实数集![]() ”为事件
”为事件![]() ,求事件
,求事件![]() 发生的概率.
发生的概率.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com