
【题目】已知点F1、F2为双曲线C:x2﹣ ![]() =1的左、右焦点,过F2作垂直于x轴的直线,在x轴上方交双曲线C于点M,∠MF1F2=30°.
=1的左、右焦点,过F2作垂直于x轴的直线,在x轴上方交双曲线C于点M,∠MF1F2=30°.
(1)求双曲线C的方程;
(2)过双曲线C上任意一点P作该双曲线两条渐近线的垂线,垂足分别为P1、P2 , 求 ![]() 的值.
的值.
【答案】
(1)解:设F2,M的坐标分别为 ![]() ,
,
因为点M在双曲线C上,所以 ![]() ,即
,即 ![]() ,所以
,所以 ![]() ,
,
在Rt△MF2F1中,∠MF1F2=30°, ![]() ,所以
,所以 ![]()
由双曲线的定义可知: ![]()
故双曲线C的方程为: ![]()
(2)解:由条件可知:两条渐近线分别为 ![]()
设双曲线C上的点Q(x0,y0),设两渐近线的夹角为θ,
则点Q到两条渐近线的距离分别为 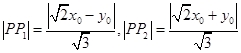 ,
,
因为Q(x0,y0)在双曲线C: ![]() 上,
上,
所以 ![]() ,又cosθ=﹣
,又cosθ=﹣ ![]() ,
,
所以 ![]() =﹣
=﹣ 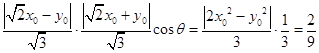
【解析】(1)设F2 , M的坐标分别为 ![]() ,求出|MF2|,Rt△MF2F1中,∠MF1F2=30°,求出|MF1|,利用双曲线的定义,即可求双曲线C的方程;(2)求出两条渐近线方程,可得点Q到两条渐近线的距离,设两渐近线的夹角为θ,可得
,求出|MF2|,Rt△MF2F1中,∠MF1F2=30°,求出|MF1|,利用双曲线的定义,即可求双曲线C的方程;(2)求出两条渐近线方程,可得点Q到两条渐近线的距离,设两渐近线的夹角为θ,可得 ![]() ,利用向量的数量积公式,即可求
,利用向量的数量积公式,即可求 ![]() 的值.
的值.


 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案科目:高中数学 来源: 题型:
【题目】下面给出一个问题的算法:
S1 输入x;
S2 若x≤2,则执行S3;否则,执行S4;
S3 输出-2x-1;
S4 输出x2-6x+3.
问题:
(1)这个算法解决的是什么问题?
(2)当输入的x值为多大时,输出的数值最小?
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,正方体![]() 的棱长为
的棱长为![]() ,
, ![]() 为
为![]() 的中点,
的中点, ![]() 为线段
为线段![]() 上的动点,过点
上的动点,过点![]() ,
, ![]() ,
, ![]() 的平面截该正方体所得的截面为
的平面截该正方体所得的截面为![]() ,则下列命题正确的是__________(写出所有正确命题的编号).
,则下列命题正确的是__________(写出所有正确命题的编号).

①当![]() 时,
时, ![]() 为四边形;②当
为四边形;②当![]() 时,
时, ![]() 为等腰梯形;
为等腰梯形;
③当![]() 时,
时, ![]() 与
与![]() 的交点
的交点![]() 满足
满足![]() ;
;
④当![]() 时,
时, ![]() 为五边形;
为五边形;
⑤当![]() 时,
时, ![]() 的面积为
的面积为![]() .
.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某车间将![]() 名技工平均分成甲、乙两组加工某种零件,在单位时间内每个技工加工的合格零件数的茎叶图如图,已知两组技工在单位时间内加工的合格零件的平均数都为
名技工平均分成甲、乙两组加工某种零件,在单位时间内每个技工加工的合格零件数的茎叶图如图,已知两组技工在单位时间内加工的合格零件的平均数都为![]() .
.

(1)求![]() ,
,![]() 的值;
的值;
(2)求甲、乙两组技工在单位时间内加工的合格零件的方差![]() 和
和![]() ,并由此分析两组技工的加工水平;
,并由此分析两组技工的加工水平;
(3)质检部门从该车间甲、乙两组技工中各随机抽取一名,对其加工的零件进行检测,若两人加工的合格零件个数之和大于![]() ,则称该车间“质量合格”,求该车间“质量合格”的概率.
,则称该车间“质量合格”,求该车间“质量合格”的概率.
附:方差![]() ,其中
,其中![]() 为数据
为数据![]() 的平均数
的平均数
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com