考点:分段函数的应用
专题:函数的性质及应用
分析:作出函数f(x)的图象,根据图象可得函数的单调性,易知3-x2≤3,分情况讨论:解不等式即可;
解答:
解:作出函数f(x)的图象,如右图所示:二次函数的对称轴为x=3,
显然3-x
2≤3,
①当2x≤3时,由图象知f(x)在(-∞,3]上递减,在[3,+∞)上递增,
由f(3-x
2)<f(2x)得3-x
2>2x,
从而可得不等式组
,即
,解得-3<x<1,
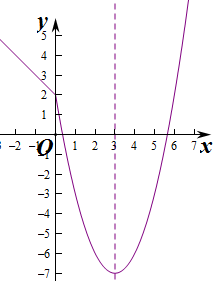
②当2x>3时,若3-x
2≥0,由y=x
2-6x+2的图象关于x=3对称,得f(3-x
2)=f[6-(3-x
2)]=f(3+x
2),
则f(3-x
2)<f(2x),
即f(3+x
2)<f(2x),
由图象知f(x)在[3,+∞)上递增,有3+x
2<2x,
所以有不等式组
,此时无解;
③当2x>3时,若3-x
2<0,由f(3-x
2)<f(2x),
得2-(3-x
2)<(2x)
2-6×2x+2,化简得x
2-4x+1>0,
从而可得不等式组
,解得x>2+
;
综上可得f(3-x
2)<f(2x)的解集为:(-3,1)∪(2+
,+∞).
点评:本题考查二次函数的单调性及其应用,考查不等式的求解,考查分类讨论思想、数形结合思想,考查学生分析解决问题的能力.

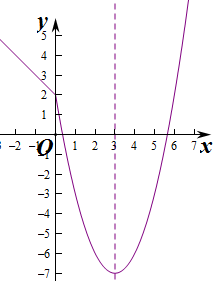


 期末1卷素质教育评估卷系列答案
期末1卷素质教育评估卷系列答案 如图,现有一块半径为2m,圆心角为90°的扇形铁皮AOB,欲从其中裁剪出一块内接五边形ONPQR,使点P在AB弧上,点M,N分别在半径OA和OB上,四边形PMON是矩形,点Q在弧AP上,R点在线段AM上,四边形PQRM是直角梯形.现有如下裁剪方案:先使矩形PMON的面积达到最大,在此前提下,再使直角梯形PQRM的面积也达到最大:求出裁剪出的五边形的面积.
如图,现有一块半径为2m,圆心角为90°的扇形铁皮AOB,欲从其中裁剪出一块内接五边形ONPQR,使点P在AB弧上,点M,N分别在半径OA和OB上,四边形PMON是矩形,点Q在弧AP上,R点在线段AM上,四边形PQRM是直角梯形.现有如下裁剪方案:先使矩形PMON的面积达到最大,在此前提下,再使直角梯形PQRM的面积也达到最大:求出裁剪出的五边形的面积.