
从0,1,2, ,10中挑选若干个不同的数字填满图中每一个圆圈称为一种“填法”,若各条线段相连的两个圆圈内的数字之差的绝对值各不相同,则称这样的填法为“完美填法”。
试问:对图1和图2是否存在完美填法?若存在,请给出一种完美填法;若不存在,请说明理由。

科目:高中数学 来源: 题型:解答题
设 是由
是由 个实数组成的
个实数组成的 行
行 列的数表,如果某一行(或某一列)各数之和为负数,则改变该行(或该列)中所有数的符号,称为一次“操作”.
列的数表,如果某一行(或某一列)各数之和为负数,则改变该行(或该列)中所有数的符号,称为一次“操作”.
(Ⅰ) 数表 如表1所示,若经过两次“操作”,使得到的数表每行的各数之和与每列的各数之和均为非负实数,请写出每次“操作”后所得的数表(写出一种方法即可);
如表1所示,若经过两次“操作”,使得到的数表每行的各数之和与每列的各数之和均为非负实数,请写出每次“操作”后所得的数表(写出一种方法即可);
表1
| 1 | 2 | 3 |  |
 | 1 | 0 | 1 |
 如表2所示,若经过任意一次“操作”以后,便可使得到的数表每行的各数之和与每列的各数之和均为非负整数,求整数
如表2所示,若经过任意一次“操作”以后,便可使得到的数表每行的各数之和与每列的各数之和均为非负整数,求整数 的所有可能值;
的所有可能值;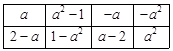
 个整数组成的
个整数组成的 行
行 列的任意一个数表
列的任意一个数表 ,能否经过有限次“操作”以后,使得到的数表每行的各数之和与每列的各数之和均为非负整数?请说明理由.
,能否经过有限次“操作”以后,使得到的数表每行的各数之和与每列的各数之和均为非负整数?请说明理由. 查看答案和解析>>
科目:高中数学 来源: 题型:单选题
若(a-4i)i=b-i,(a,b∈R,i为虚数单位),则复数z=a+bi在复平面内的对应点位于( )
| A.第一象限 | B.第二象限 | C.第三象限 | D.第四象限 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com