
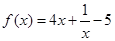 ,②
,②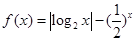 ,③
,③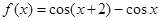 ,判断如下两个命题的真假:
,判断如下两个命题的真假: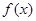 在区间
在区间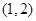 上是增函数;
上是增函数;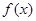 在区间
在区间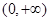 上恰有两个零点
上恰有两个零点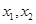 ,且
,且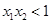 .能使命题甲、乙均为真的函数的序号是
.能使命题甲、乙均为真的函数的序号是| A.① | B.② | C.①③ | D.①② |
 )x的和函数,且两者在区间(1,2)上均是增函数,知f(x)=|log2x|-(
)x的和函数,且两者在区间(1,2)上均是增函数,知f(x)=|log2x|-(  )x是增函数.③f(x)=0得cos(x+2)=cosx,在(0,+∞)上无数个零点.
)x是增函数.③f(x)=0得cos(x+2)=cosx,在(0,+∞)上无数个零点. ,在区间(1,2)f’(x)>0,f(x)在区间(1,2)上是增函数.使甲为真.f(x)的最小值是-1<0当x=
,在区间(1,2)f’(x)>0,f(x)在区间(1,2)上是增函数.使甲为真.f(x)的最小值是-1<0当x= 时取得.又f(1)=0,∴f(x)在区间(0,+∞)上恰有两个零点x1<
时取得.又f(1)=0,∴f(x)在区间(0,+∞)上恰有两个零点x1< ;x2=1. x1x2=x1<1,使乙为真.
;x2=1. x1x2=x1<1,使乙为真. )x也是增函数,两者的和函数也是增函数.使甲为真.利用信息技术f(x)在区间(0,+∞)上恰有两个零点x1,x2;0<x1<
)x也是增函数,两者的和函数也是增函数.使甲为真.利用信息技术f(x)在区间(0,+∞)上恰有两个零点x1,x2;0<x1<


科目:高中数学 来源:不详 题型:填空题
 ,
, , 平面
, 平面 ,
, ,
, ,给出下列四个命题:
,给出下列四个命题: ∥
∥ ,
, ⊥
⊥ ,
, ∥
∥ ,则
,则 ⊥
⊥ ;
;  ∥
∥ ,
,  ∥
∥ ,
, ∥
∥ ,则
,则 ∥
∥ ;
; ⊥
⊥ ,
,  ⊥
⊥ ,则
,则 ∥
∥ ;
;  ∥
∥ ,
, ∥
∥ ,
,  ∩
∩ =
= ,则
,则 ∥
∥ .
.查看答案和解析>>
科目:高中数学 来源:不详 题型:填空题
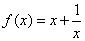 的值域是(-∞,-2]∪[2,+∞);
的值域是(-∞,-2]∪[2,+∞);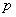 与命题
与命题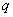 ,若
,若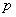 是
是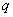 的充分不必要条件,则
的充分不必要条件,则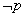 是
是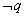 的充分不必要条件
的充分不必要条件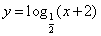 的图象经过第一象限;
的图象经过第一象限;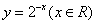 的反函数是
的反函数是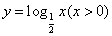 ;
;查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com