
 新课标阶梯阅读训练系列答案
新课标阶梯阅读训练系列答案科目:高中数学 来源: 题型:
查看答案和解析>>
科目:高中数学 来源: 题型:
| y-3 |
| x-2 |
| y-1 |
| x+3 |
| x2 |
| 2+m |
| y2 |
| m+1 |
查看答案和解析>>
科目:高中数学 来源: 题型:
 (2012•湖南模拟)选做题(请考生在第16题的三个小题中任选两题作答,如果全做,则按前两题记分,要写出必要的推理与演算过程)
(2012•湖南模拟)选做题(请考生在第16题的三个小题中任选两题作答,如果全做,则按前两题记分,要写出必要的推理与演算过程)
|
| a2 |
| x |
| b2 |
| y |
| (a+b)2 |
| x+y |
| a |
| x |
| b |
| y |
| 2 |
| x |
| 9 |
| 1-2x |
| 1 |
| 2 |
查看答案和解析>>
科目:高中数学 来源:2012-2013学年辽宁省高三第五次模拟理数试卷(解析版) 题型:填空题
下列命题中正确的是 .
①如果幂函数 的图象不过原点,则m=1或m=2;
的图象不过原点,则m=1或m=2;
②定义域为R的函数一定可以表示成一个奇函数与一个偶函数的和;
③已知直线a、b、c两两异面,则与a、b、c同时相交的直线有无数条;
④方程 =
= 表示经过点A(2,3)、B(-3,1)的直线;
表示经过点A(2,3)、B(-3,1)的直线;
⑤方程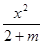 -
- =1表示的曲线不可能是椭圆;
=1表示的曲线不可能是椭圆;
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com