
����Ŀ��һ����������A,B,C����γ�,ÿ��γ����������ͺͱ��������ͺ�,ij�µIJ��������ʾ(��λ��)������A,B,C�����÷ֲ�����ķ���������������Ľγ��г�ȡ50��,��A��γ���10��
�γ�A | �γ�B | �γ�C | |
������ | 100 | 150 | z |
���� | 300 | 450 | 600 |
��1�����±���z��ֵ��
��2������������ķ�����B�������ͽγ��г�ȡ8��,��������ǵĵ÷����£�94,86,92,96,87,93,90,82����8���γ��ĵ÷ֿ���һ������,������ȡһ���÷���![]() ����8���γ��ĵ÷ֵ�ƽ����Ϊ
����8���γ��ĵ÷ֵ�ƽ����Ϊ![]() �������¼�
�������¼�![]() {
{![]() ���Һ���
���Һ���![]() û�����}�����¼�
û�����}�����¼�![]() �����ĸ���
�����ĸ���
���𰸡�(1)400��(2)![]() .
.
��������
���⣨1����ó����������γ�Ϊn����������ã�![]() �����
�����![]() ���ɵ�
���ɵ�![]() ��ֵ ��2�� ���8���γ��ĵ÷ֵ�ƽ����Ϊ
��ֵ ��2�� ���8���γ��ĵ÷ֵ�ƽ����Ϊ![]() ����
����![]() ���Һ���
���Һ���![]() û����� �ɵ�
û����� �ɵ�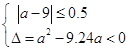 ���ɴ˽��
���ɴ˽��![]() �ķ�Χ�����
�ķ�Χ�����![]() �������ҽ���
�������ҽ���![]() ��ֵ���Ӷ�����¼�
��ֵ���Ӷ�����¼�![]() �����ĸ���
�����ĸ���
�����������1����ó����������γ�Ϊ![]() ��,�������
��,�������![]() ,����
,����![]()
![]() =2000-100-300-150-450-600=400 4��
=2000-100-300-150-450-600=400 4��
��2�� 8���γ��ĵ÷ֵ�ƽ����Ϊ![]() 6��
6��
��8���γ��ĵ÷ֿ���һ������,������ȡһ������![]() ��Ӧ�Ļ����¼�������Ϊ
��Ӧ�Ļ����¼�������Ϊ![]() ��,
��,
��![]() ���Һ���
���Һ���![]() û�����
û�����
 10��
10��
![]()
![]() �������ҽ���
�������ҽ���![]() ��ֵΪ��8 6, 9 2, 8 7, 9 0��4��,
��ֵΪ��8 6, 9 2, 8 7, 9 0��4��,
![]() 12��
12��


 �ƸԿ�����ҵ��ϵ�д�
�ƸԿ�����ҵ��ϵ�д� ��Ԫ����ĩ��ϰ�ȷ��ϵ�д�
��Ԫ����ĩ��ϰ�ȷ��ϵ�д�
| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ��ijѧУΪ�˽�ѧ����ʳ���ò͵�����ȣ���ȫУ��ʳ���ò͵�3000��ѧ���У������ȡ100��ѧ����ʳ���ò͵�����Ƚ������֣�����ѧ����ʳ���ò�����ȵ����֣��õ���ͼ��ʾ��Ƶ�ʷֲ�ֱ��ͼ��
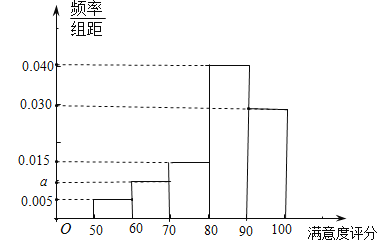
��1����Ƶ�ʷֲ�ֱ��ͼ��a��ֵ������������λ��
��2���涨��ѧ����ʳ���ò�����ȵ����ֲ�����80��Ϊ�������������Թ��Ƹ�У��ʳ���ò͵�3000��ѧ��������������������.
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ѡ��4-4������ϵ��������̣�
��֪����C�ļ����귽������=2cos�����Լ���Ϊƽ��ֱ������ϵ��ԭ�㣬����Ϊx��������ᣬ����ƽ��ֱ������ϵ��ֱ��L�IJ���������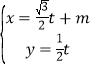 ��tΪ��������
��t��������
��1��������C��ֱ�����귽�̺�ֱ��L����ͨ���̣�
��2�����P��m��0������ֱ��L������C����A��B���㣬��|PA||PB|=1����ʵ��m��ֵ��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
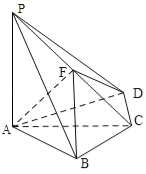
����Ŀ����ͼ������P��ABCD�У�PA������ABCD��BC=CD=2��AC=4����ACB=��ACD=![]() ��FΪPC���е㣬AF��PB��
��FΪPC���е㣬AF��PB��
��1����PA�ij���
��2��������B��AF��D������ֵ��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ���Գ���Ϊֱ��![]() �������߾�����
�������߾�����![]() ��
��![]() .
.
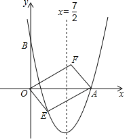
��1���������߽���ʽ���������ꣻ
��2�����![]() ����������һ���㣬��λ�ڵ������ޣ��ı���OEAF����OAΪ�Խ��ߵ�ƽ���ı��Σ����ı���OEAF�����S��x֮��ĺ�����ϵʽ����д���Ա���x��ȡֵ��Χ��
����������һ���㣬��λ�ڵ������ޣ��ı���OEAF����OAΪ�Խ��ߵ�ƽ���ı��Σ����ı���OEAF�����S��x֮��ĺ�����ϵʽ����д���Ա���x��ȡֵ��Χ��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����![]() �ķ�����У�ÿ����Ⱦ�Ϻ졢�����ơ���������ɫ֮һ����ÿ��
�ķ�����У�ÿ����Ⱦ�Ϻ졢�����ơ���������ɫ֮һ����ÿ��![]() ���ӷ��������ÿ����ɫ�ĸ��Ϊһ���ƴ�Ⱦ��Ϊ�����⡱�ģ������в�ͬ�ľ����Ⱦ����__________�֣�
���ӷ��������ÿ����ɫ�ĸ��Ϊһ���ƴ�Ⱦ��Ϊ�����⡱�ģ������в�ͬ�ľ����Ⱦ����__________�֣�
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����֪��������![]() ��ǰn���Ϊ
��ǰn���Ϊ![]() ������
������![]() ��
��![]() .
.
��1��������![]() ��ͨ�ʽ����
��ͨ�ʽ����![]() ���������k�ķ�Χ��
���������k�ķ�Χ��
��2����![]() ����
����![]() �ǵ������У���ʵ��a��ȡֵ��Χ.
�ǵ������У���ʵ��a��ȡֵ��Χ.
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����֪����![]() ,����
,����![]() .
.
(1)����![]() ������
������![]() �ϵĵ�����;
�ϵĵ�����;
(2)��![]() ����������ֵ��
����������ֵ��![]() ,��
,��![]() ,��
,��![]() ��ȡֵ��Χ.
��ȡֵ��Χ.
�鿴�𰸺ͽ���>>
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com