
ЁОЬтФПЁПжкЫљжмжЊЕФЁАЬЋМЋЭМЁБЃЌЦфаЮзДШчЖдГЦЕФвѕбєСНгуЛЅБЇдквЛЦ№ЃЌвВБЛГЦЮЊЁАвѕбєгуЬЋМЋЭМЁБЃЎШчЭМЪЧЗХдкЦНУцжБНЧзјБъЯЕжаЕФЁАЬЋМЋЭМЁБЃЎећИіЭМаЮЪЧвЛИідВаЮЃЎЦфжаКкЩЋвѕгАЧјгђдкyжсгвВрВПЗжЕФБпНчЮЊвЛИіАыдВЃЌИјГівдЯТУќЬтЃК
ЂйдкЬЋМЋЭМжаЫцЛњШЁвЛЕуЃЌДЫЕуШЁздКкЩЋвѕгАВПЗжЕФИХТЪЪЧ![]()
ЂкЕБ![]() ЪБЃЌжБЯпyЃНax+2aгыАзЩЋВПЗжгаЙЋЙВЕуЃЛ
ЪБЃЌжБЯпyЃНax+2aгыАзЩЋВПЗжгаЙЋЙВЕуЃЛ
ЂлКкЩЋвѕгАВПЗжЃЈАќРЈКкАзНЛНчДІЃЉжавЛЕуЃЈxЃЌyЃЉЃЌдђx+yЕФзюДѓжЕЮЊ2ЃЛ
ЂмЩшЕуPЃЈЉ2ЃЌbЃЉЃЌЕуQдкДЫЬЋМЋЭМЩЯЃЌЪЙЕУЁЯOPQЃН45ЁуЃЌbЕФЗЖЮЇЪЧ[Љ2ЃЌ2]ЃЎ
ЦфжаЫљгае§ШЗНсТлЕФађКХЪЧЃЈ ЃЉ
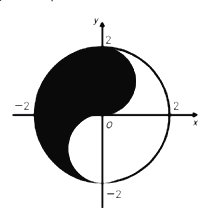
A.ЂйЂмB.ЂйЂлC.ЂкЂмD.ЂйЂк
ЁОД№АИЁПA
ЁОНтЮіЁП
ИљОнМИКЮИХаЭИХТЪМЦЫуЃЌХаЖЯЂйЕФжмЦкад.ИљОнжБЯп![]() КЭдВ
КЭдВ![]() ЕФЮЛжУЙиЯЕЃЌХаЖЯЂкЕФе§ШЗад.ИљОнЯпадЙцЛЎЕФжЊЪЖЧѓЕУ
ЕФЮЛжУЙиЯЕЃЌХаЖЯЂкЕФе§ШЗад.ИљОнЯпадЙцЛЎЕФжЊЪЖЧѓЕУ![]() ЕФзюДѓжЕЃЌгЩДЫХаЖЯЂлЕФе§ШЗад.НЋ
ЕФзюДѓжЕЃЌгЩДЫХаЖЯЂлЕФе§ШЗад.НЋ![]() зЊЛЏЮЊЙ§
зЊЛЏЮЊЙ§![]() ЕФСНЬѕЧаЯпЫљГЩЕФНЧДѓгкЕШгк
ЕФСНЬѕЧаЯпЫљГЩЕФНЧДѓгкЕШгк![]() ЃЌгЩДЫЧѓЕУ
ЃЌгЩДЫЧѓЕУ![]() ЕФШЁжЕЗЖЮЇЃЌНјЖјЧѓЕУ
ЕФШЁжЕЗЖЮЇЃЌНјЖјЧѓЕУ![]() ЕФШЁжЕЗЖЮЇЃЌДгЖјХаЖЯГіЂмЕФе§ШЗад.
ЕФШЁжЕЗЖЮЇЃЌДгЖјХаЖЯГіЂмЕФе§ШЗад.
ЖдгкЂйЃЌНЋyжсгвВрКкЩЋвѕгАВПЗжВЙЕНзѓВрЃЌМДПЩжЊКкЩЋвѕгАЧјгђеМдВЕФУцЛ§ЕФвЛАыЃЌ
ИљОнМИКЮИХаЭЕФМЦЫуЙЋЪНЃЌЫљвддкЬЋМЋЭМжаЫцЛњШЁвЛЕуЃЌДЫЕуШЁздКкЩЋвѕгАВПЗжЕФИХТЪЪЧ![]() ЃЌе§ШЗЃЛ
ЃЌе§ШЗЃЛ
ЖдгкЂкЃЌЕБ![]() ЪБЃЌжБЯп
ЪБЃЌжБЯп![]() ,Й§Еу
,Й§Еу![]() ЃЌЫљвджБЯп
ЃЌЫљвджБЯп![]() гыАзЩЋВПЗждкЕкIКЭЕкIVЯѓЯоВПЗжУЛгаЙЋЙВЕу.дВ
гыАзЩЋВПЗждкЕкIКЭЕкIVЯѓЯоВПЗжУЛгаЙЋЙВЕу.дВ![]() ЕФдВаФЮЊ
ЕФдВаФЮЊ![]() ЃЌАыОЖЮЊ
ЃЌАыОЖЮЊ![]() ЃЌдВаФ
ЃЌдВаФ![]() ЕНжБЯп
ЕНжБЯп![]() ЃЌМДжБЯп
ЃЌМДжБЯп![]() ЕФОрРыЮЊ
ЕФОрРыЮЊ![]() ЃЌЫљвджБЯп
ЃЌЫљвджБЯп![]() гыАзЩЋВПЗждкЕкIIIЯѓЯоЕФВПЗжУЛгаЙЋЙВЕу.злЩЯЫљЪіЃЌжБЯпyЃНax+2aгыАзЩЋВПЗжУЛгаЙЋЙВЕуЃЌЂкДэЮѓЃЛ
гыАзЩЋВПЗждкЕкIIIЯѓЯоЕФВПЗжУЛгаЙЋЙВЕу.злЩЯЫљЪіЃЌжБЯпyЃНax+2aгыАзЩЋВПЗжУЛгаЙЋЙВЕуЃЌЂкДэЮѓЃЛ
ЖдгкЂлЃЌЩшlЃКzЃНx+yЃЌгЩЯпадЙцЛЎжЊЪЖПЩжЊЃЌЕБжБЯпlгыдВx2+ЃЈyЉ1ЃЉ2ЃН1ЯрЧаЪБЃЌzзюДѓЃЌ
гЩ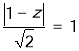 НтЕУz
НтЕУz![]() ЃЈ
ЃЈ![]() ЩсШЅЃЉЃЌЂлДэЮѓЃЛ
ЩсШЅЃЉЃЌЂлДэЮѓЃЛ
ЖдгкЂмЃЌвЊЪЙЕУЁЯOPQЃН45ЁуЃЌМДашвЊЙ§ЕуPЕФСНЬѕЧаЯпЫљГЩНЧДѓгкЕШгк![]() ЃЌ
ЃЌ
Ыљвд![]() ЃЌМДOPЁм2
ЃЌМДOPЁм2![]() ЃЌгкЪЧ22+b2Ём8ЃЌНтЕУ
ЃЌгкЪЧ22+b2Ём8ЃЌНтЕУ![]() ЃЎ
ЃЎ
ЙЪбЁЃКA



| ФъМЖ | ИпжаПЮГЬ | ФъМЖ | ГѕжаПЮГЬ |
| ИпвЛ | ИпвЛУтЗбПЮГЬЭЦМіЃЁ | ГѕвЛ | ГѕвЛУтЗбПЮГЬЭЦМіЃЁ |
| ИпЖў | ИпЖўУтЗбПЮГЬЭЦМіЃЁ | ГѕЖў | ГѕЖўУтЗбПЮГЬЭЦМіЃЁ |
| ИпШ§ | ИпШ§УтЗбПЮГЬЭЦМіЃЁ | ГѕШ§ | ГѕШ§УтЗбПЮГЬЭЦМіЃЁ |
ПЦФПЃКИпжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПЙигк![]() ЕФВЛЕШЪН
ЕФВЛЕШЪН![]() ЃЌЖдгк
ЃЌЖдгк![]() КуГЩСЂЃЌдђЪЕЪ§
КуГЩСЂЃЌдђЪЕЪ§![]() ЕФШЁжЕЗЖЮЇЪЧ________.
ЕФШЁжЕЗЖЮЇЪЧ________.
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКИпжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПвбжЊКЏЪ§fЃЈxЃЉЃНxlnxЃЌКЏЪ§gЃЈxЃЉЃНkxЉcosxдкЕу![]() ДІЕФЧаЯпЦНаагкxжс.
ДІЕФЧаЯпЦНаагкxжс.
ЃЈ1ЃЉЧѓКЏЪ§fЃЈxЃЉЕФМЋжЕЃЛ
ЃЈ2ЃЉЬжТлКЏЪ§FЃЈxЃЉЃНgЃЈxЃЉЉfЃЈxЃЉЕФСуЕуЕФИіЪ§.
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКИпжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПФГЩчЧјЯћЗбепаЛсЮЊСЫНтБОЩчЧјОгУёЭјЙКЯћЗбЧщПіЃЌЫцЛњГщШЁСЫ100ЮЛОгУёзїЮЊбљБОЃЌОЭзюНќвЛФъРДЭјЙКЯћЗбН№Жю(ЕЅЮЛЃКЧЇдЊ)ЃЌЭјЙКДЮЪ§КЭжЇИЖЗНЪНЕШНјааСЫЮЪОэЕїЫ.ОЭГМЦет100ЮЛОгУёЕФЭјЙКЯћЗбН№ЖюОљдкЧјМф![]() ФкЃЌАД
ФкЃЌАД![]() ЃЌ
ЃЌ![]() ЃЌ
ЃЌ![]() ЃЌ
ЃЌ![]() ЃЌ
ЃЌ![]() ЃЌ
ЃЌ![]() ЗжГЩ6зщЃЌЦфЦЕТЪЗжВМжБЗНЭМШчЭМЫљЪО.
ЗжГЩ6зщЃЌЦфЦЕТЪЗжВМжБЗНЭМШчЭМЫљЪО.
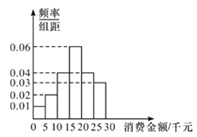
ЃЈ1ЃЉЙРМЦИУЩчЧјОгУёзюНќвЛФъРДЭјЙКЯћЗбН№ЖюЕФжаЮЛЪ§ЃЛ
ЃЈ2ЃЉНЋЭјЙКЯћЗбН№Жюдк20ЧЇдЊвдЩЯепГЦЮЊЁАЭјЙКУдЁБЃЌВЙШЋЯТУцЕФ![]() СаСЊБэЃЌВЂХаЖЯгаЖрДѓАбЮеШЯЮЊЁАЭјЙКУдгыадБ№гаЙиЯЕЁБЃЛ
СаСЊБэЃЌВЂХаЖЯгаЖрДѓАбЮеШЯЮЊЁАЭјЙКУдгыадБ№гаЙиЯЕЁБЃЛ
Фа | ХЎ | КЯМЦ | |
ЭјЙКУд | 20 | ||
ЗЧЭјЙКУд | 45 | ||
КЯМЦ | 100 |
ЃЈ3ЃЉЕїЫЯдЪОЃЌМзЁЂввСНШЫУПДЮЭјЙКВЩгУЕФжЇИЖЗНЪНЯрЛЅЖРСЂЃЌСНШЫЭјЙКЪБМфгыДЮЪ§вВЛЅВЛ. гАЯь.ЭГМЦзюНќвЛФъРДСНШЫЭјЙКЕФзмДЮЪ§гыжЇИЖЗНЪНЃЌЫљЕУЪ§ОнШчЯТБэЫљЪОЃК
ЭјЙКзмДЮЪ§ | жЇИЖБІжЇИЖДЮЪ§ | вјааПЈжЇИЖДЮЪ§ | ЮЂаХжЇИЖДЮЪ§ | |
Мз | 80 | 40 | 16 | 24 |
вв | 90 | 60 | 18 | 12 |
НЋЦЕТЪЪгЮЊИХТЪЃЌШєМзЁЂввСНШЫдкЯТжмФкИїздЭјЙК2ДЮЃЌМЧСНШЫВЩгУжЇИЖБІжЇИЖЕФДЮЪ§жЎКЭЮЊ![]() ЃЌЧѓ
ЃЌЧѓ![]() ЕФЪ§бЇЦкЭћ.
ЕФЪ§бЇЦкЭћ.
ИНЃКЙлВтжЕЙЋЪНЃК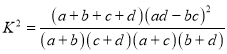
СйНчжЕБэЃК
| 0.01 | 0.05 | 0.025 | 0.010 | 0.005 | 0.001 |
| 2.706 | 3.841 | 5.024 | 6.635 | 7.879 | 10.828 |
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКИпжаЪ§бЇ РДдДЃК ЬтаЭЃК
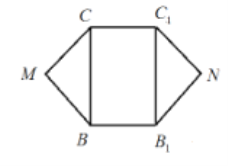
ЁОЬтФПЁПЦНУцЭЙСљБпаЮ![]() ЕФБпГЄЯрЕШ,Цфжа
ЕФБпГЄЯрЕШ,Цфжа![]() ЮЊОиаЮ,
ЮЊОиаЮ,![]() ЃЎНЋ
ЃЎНЋ![]() ,
,![]() ЗжБ№би
ЗжБ№би![]() ,
,![]() елжС
елжС![]() ,
,![]() ,ЧвОљдкЭЌВргыЦНУц
,ЧвОљдкЭЌВргыЦНУц![]() ДЙжБ,СЌНг
ДЙжБ,СЌНг![]() ,ШчЭМЫљЪО,E,GЗжБ№ЪЧ
,ШчЭМЫљЪО,E,GЗжБ№ЪЧ![]() ,
,![]() ЕФжаЕуЃЎ
ЕФжаЕуЃЎ
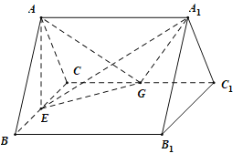
ЃЈ1ЃЉЧѓжЄЃКЖрУцЬх![]() ЮЊжБШ§РтжљЃЛ
ЮЊжБШ§РтжљЃЛ
ЃЈ2ЃЉЧѓЖўУцНЧ![]() ЦНУцНЧЕФгрЯвжЕЃЎ
ЦНУцНЧЕФгрЯвжЕЃЎ
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКИпжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПвбжЊКЏЪ§fЃЈxЃЉЃНaxexЃЌgЃЈxЃЉЃНx2+2x+bЃЌШєЧњЯпyЃНfЃЈxЃЉгыЧњЯпyЃНgЃЈxЃЉЖМЙ§ЕуPЃЈ1ЃЌcЃЉЃЎЧвдкЕуPДІгаЯрЭЌЕФЧаЯпlЃЎ
ЃЈЂёЃЉЧѓЧаЯпlЕФЗНГЬЃЛ
ЃЈЂђЃЉШєЙигкxЕФВЛЕШЪНk[efЃЈxЃЉ]ЁнgЃЈxЃЉЖдШЮвтxЁЪ[Љ1ЃЌ+ЁоЃЉКуГЩСЂЃЌЧѓЪЕЪ§kЕФШЁжЕЗЖЮЇЃЎ
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКИпжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПвбжЊЭждВ![]()
![]() ЕФРыаФТЪЮЊ
ЕФРыаФТЪЮЊ![]() ЃЌНЙОрЮЊ
ЃЌНЙОрЮЊ![]() ЃЌжБЯп
ЃЌжБЯп![]() Й§ЭждВЕФ
Й§ЭждВЕФ![]() зѓНЙЕу.
зѓНЙЕу.
ЃЈ1ЃЉЧѓЭждВ![]() ЕФБъзМЗНГЬЃЛ
ЕФБъзМЗНГЬЃЛ
ЃЈ2ЃЉШєжБЯп![]() гы
гы![]() жсНЛгкЕу
жсНЛгкЕу![]() ЪЧЭждВ
ЪЧЭждВ![]() ЩЯЕФСНИіЖЏЕу,
ЩЯЕФСНИіЖЏЕу,![]() ЕФЦНЗжЯпдк
ЕФЦНЗжЯпдк![]() жсЩЯ,
жсЩЯ,![]() .ЪдХаЖЯжБЯп
.ЪдХаЖЯжБЯп![]() ЪЧЗёЙ§ЖЈЕуЃЌШєЙ§ЖЈЕуЃЌЧѓГіЖЈЕузјБъ;ШєВЛЙ§ЖЈЕуЃЌЧыЫЕУїРэгЩ.
ЪЧЗёЙ§ЖЈЕуЃЌШєЙ§ЖЈЕуЃЌЧѓГіЖЈЕузјБъ;ШєВЛЙ§ЖЈЕуЃЌЧыЫЕУїРэгЩ.
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКИпжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПвбжЊКЏЪ§fЃЈxЃЉ![]() |2xЉ3|ЃЌgЃЈxЃЉ
|2xЉ3|ЃЌgЃЈxЃЉ![]() |2x+a+b|.
|2x+a+b|.
ЃЈ1ЃЉНтВЛЕШЪНfЃЈxЃЉ![]() x2ЃЛ
x2ЃЛ
ЃЈ2ЃЉЕБa![]() 0ЃЌb
0ЃЌb![]() 0ЪБЃЌШєFЃЈxЃЉ
0ЪБЃЌШєFЃЈxЃЉ![]() fЃЈxЃЉ+gЃЈxЃЉЕФжЕгђЮЊ[5ЃЌ+ЁоЃЉЃЌЧѓжЄЃК
fЃЈxЃЉ+gЃЈxЃЉЕФжЕгђЮЊ[5ЃЌ+ЁоЃЉЃЌЧѓжЄЃК![]() .
.
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКИпжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПШєЪ§Са![]() ТњзуnЁн2ЪБЃЌ
ТњзуnЁн2ЪБЃЌ![]() ЃЌдђГЦЪ§Са
ЃЌдђГЦЪ§Са![]() (n
(n![]() )ЮЊ
)ЮЊ![]() ЕФЁАLЪ§СаЁБЃЎ
ЕФЁАLЪ§СаЁБЃЎ
ЃЈ1ЃЉШє![]() ЃЌЧв
ЃЌЧв![]() ЕФЁАLЪ§СаЁБЮЊ
ЕФЁАLЪ§СаЁБЮЊ![]() ЃЌЧѓЪ§Са
ЃЌЧѓЪ§Са![]() ЕФЭЈЯюЙЋЪНЃЛ
ЕФЭЈЯюЙЋЪНЃЛ
ЃЈ2ЃЉШє![]() ЃЌЧв
ЃЌЧв![]() ЕФЁАLЪ§СаЁБЮЊЕндіЪ§СаЃЌЧѓkЕФШЁжЕЗЖЮЇЃЛ
ЕФЁАLЪ§СаЁБЮЊЕндіЪ§СаЃЌЧѓkЕФШЁжЕЗЖЮЇЃЛ
ЃЈ3ЃЉШє![]() ЃЌЦфжаpЃО1ЃЌМЧ
ЃЌЦфжаpЃО1ЃЌМЧ![]() ЕФЁАLЪ§СаЁБЕФЧАnЯюКЭЮЊ
ЕФЁАLЪ§СаЁБЕФЧАnЯюКЭЮЊ![]() ЃЌЪдХаЖЯЪЧЗёДцдкЕШВюЪ§Са
ЃЌЪдХаЖЯЪЧЗёДцдкЕШВюЪ§Са![]() ЃЌЖдШЮвтn
ЃЌЖдШЮвтn![]() ЃЌЖМга
ЃЌЖМга![]() ГЩСЂЃЌВЂжЄУїФуЕФНсТлЃЎ
ГЩСЂЃЌВЂжЄУїФуЕФНсТлЃЎ
ВщПДД№АИКЭНтЮі>>
АйЖШжТаХ - СЗЯАВсСаБэ - ЪдЬтСаБэ
КўББЪЁЛЅСЊЭјЮЅЗЈКЭВЛСМаХЯЂОйБЈЦНЬЈ | ЭјЩЯгаКІаХЯЂОйБЈзЈЧј | ЕчаХеЉЦОйБЈзЈЧј | ЩцРњЪЗащЮожївхгаКІаХЯЂОйБЈзЈЧј | ЩцЦѓЧжШЈОйБЈзЈЧј
ЮЅЗЈКЭВЛСМаХЯЂОйБЈЕчЛАЃК027-86699610 ОйБЈгЪЯфЃК58377363@163.com