
分析 (1)由根式内部的代数式大于等于0联立不等式组求得函数的定义域;把函数解析式两边平方,求出f2(x)的范围后得函数值域;
(2)把f2(x)、f(x)的解析式代入F(x)=$\frac{a}{2}$•[f2(x)-2]+f(x),然后令t=f(x)=$\sqrt{1+x}$+$\sqrt{1-x}$换元,化为关于t的二次函数,然后结合二次函数的性质分类求得F(x)的最大值g(a).
解答 解:(1)由$\left\{\begin{array}{l}{1+x≥0}\\{1-x≥0}\end{array}\right.$,得-1≤x≤1,∴函数f(x)的定义域为[-1,1];
又f2(x)=2+2$\sqrt{1-{x}^{2}}$∈[2,4],由f(x)≥0,得值域为[$\sqrt{2}$,2];
(2)∵F(x)=$\frac{a}{2}$•[f2(x)-2]+f(x)=a$\sqrt{1-{x}^{2}}$+$\sqrt{1+x}$+$\sqrt{1-x}$,
令t=f(x)=$\sqrt{1+x}$+$\sqrt{1-x}$,则$\sqrt{1-{x}^{2}}$=$\frac{1}{2}$t2-1,
∴F(x)=m(t)=a($\frac{1}{2}$t2-1)+t=$\frac{1}{2}$at2+t-a,t∈[$\sqrt{2}$,2],
由题意知g(a)即为函数m(t)=$\frac{1}{2}$at2+t-a,t∈[$\sqrt{2}$,2]的最大值.
注意到直线t=-$\frac{1}{a}$是抛物线mt=$\frac{1}{2}$at2+t-a的对称轴,
当a=0时,m(t)=t,∴g(a)=2;
当a>0时,m(t)=$\frac{1}{2}$at2+t-a,t∈[$\sqrt{2}$,2]递增,∴g(a)=m(2)=a+2;
当a<0时:
①若t=-$\frac{1}{a}$∈(0,$\sqrt{2}$],即a≤-$\frac{\sqrt{2}}{2}$,则g(a)=m($\sqrt{2}$)=$\sqrt{2}$;
②若t=-$\frac{1}{a}$∈($\sqrt{2}$,2],即-$\frac{\sqrt{2}}{2}$$<a≤-\frac{1}{2}$,则g(a)=m(-$\frac{1}{a}$)=-a-$\frac{1}{2a}$;
③若t=-$\frac{1}{a}$∈(2,+∞],即$-\frac{1}{2}<a<0$,则g(a)=m(2)=a+2.
综上有g(a)=$\left\{\begin{array}{l}{a+2,a≥-\frac{1}{2}}\\{-a-\frac{1}{2a},-\frac{\sqrt{2}}{2}<a<-\frac{1}{2}}\\{\sqrt{2},a≤-\frac{\sqrt{2}}{2}}\end{array}\right.$.
点评 本题考查函数的定义域及其求法,考查了利用换元法和配方法求函数的值域,体现了分类讨论的数学思想方法,属中高档题.


科目:高中数学 来源: 题型:选择题
| A. | $\frac{1}{4}$ | B. | 1 | C. | 2 | D. | 4 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | .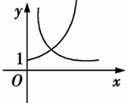 | B. | .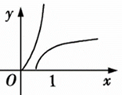 | C. | .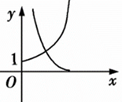 | D. | .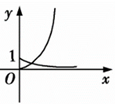 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
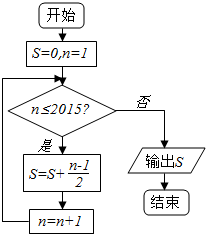
| A. | $\frac{2015×2016}{4}$ | B. | $\frac{2014×2015}{4}$ | C. | $\frac{2015×2016}{2}$ | D. | $\frac{2014×2015}{2}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $({0,\frac{π}{2}})$ | B. | (0,π) | C. | (π,2π) | D. | $({\frac{3π}{2},2π})$ |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $|{\overrightarrow a•\overrightarrow b}|≤|{\overrightarrow a}||{\overrightarrow b}|$ | B. | $|{\overrightarrow a-\overrightarrow b}|≤|{|{\overrightarrow a}|-|{\overrightarrow b}|}|$ | C. | ${(\overrightarrow a+\overrightarrow b)^2}={|{\overrightarrow a+\overrightarrow b}|^2}$ | D. | $(\overrightarrow a+\overrightarrow b)(\overrightarrow a-\overrightarrow b)={\overrightarrow a^2}-{\overrightarrow b^2}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | (-∞,-2] | B. | (-∞,0] | C. | [0,1) | D. | [-2,0] |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com