������{an}�е������ÿһ�б���һ�ж�����Ĺ����ų�����������
a1
a2a3a4
a5a6a7a8a9
��
��֪���еĵ�һ����a1��a2��a5��������һ���Ȳ����У���Ϊ{bn}����b2=4��b5=10������ÿһ�����м�һ����a1��a3��a7������������{cn}����ǰn���ΪSn��
��1��������{bn}��ͨ�ʽ��
��2�����ϱ��У��ӵڶ�����ÿһ���е����������ҵ�˳������ɵȱ����У�����Ϊͬһ����������a13=1������Sn���ڼ�M={n|��n+1��cn�ݦˣ�n��N*}��������M��Ԫ�ظ���Ϊ3����ʵ���˵�ȡֵ��Χ��
��������1����{b
n}�Ĺ���Ϊd����
���ɴ����������{b
n}��ͨ�ʽ��
��2������ÿһ����ɵĵȱ����еĹ���Ϊq������ǰn�й���1+3+5+��+��2n-1��=n
2��������3
2��13��4
2�����
q=��
cn=2n•()n-1=������
Sn=+++��+���ɴ�λ������ܹ����
Sn=8-��
����
cn=��֪����ʽ��n+1��c
n�ݦˣ��ɻ�Ϊ
�ݦ�����
f(n)=�����
f(1)=4��f(2)=f(3)=6��f(4)=5��f(5)=���ɴ��ܹ��Ƶ����˵�ȡֵ��Χ��
����⣺��1����{b
n}�Ĺ���Ϊd��
��
�����
����b
n=2n��
��2������ÿһ����ɵĵȱ����еĹ���Ϊq��
����ǰn�й���1+3+5+��+��2n-1��=n
2��������3
2��13��4
2��
��a
10=b
4=8��
��a
13=a
10q
3=8q
3��
��a
13=1�����
q=��
��
cn=2n•()n-1=��
��
Sn=+++��+��
Sn=++��++��
��
Sn=+++��+-=4-
���
Sn=8-��
���ɢ�֪��
cn=������ʽ��n+1��c
n�ݦˣ��ɻ�Ϊ
�ݦ���
��
f(n)=�����
f(1)=4��f(2)=f(3)=6��f(4)=5��f(5)=��
��n��3ʱ��f��n+1����f��n����
����M��Ԫ�ظ�����3��
��˵�ȡֵ��Χ�ǣ�4��5]��
���������⿼�����е�ͨ�ʽ����ǰn��͵ļ���͵ȱ��������ʵ�Ӧ�ã�����ʱҪע�ⷽ��˼��ʹ�λ�����ͷ��ĺ������ã�ע������ؽ��еȼ�ת����



 �Ͻ�ƽСѧ��������ϵ�д�
�Ͻ�ƽСѧ��������ϵ�д�
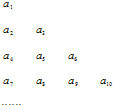 ������{an}�е������ÿһ�б���һ�ж�һ��Ĺ����ų����±���
������{an}�е������ÿһ�б���һ�ж�һ��Ĺ����ų����±���
 ������{an}�е������ÿһ�б���һ�ж�һ��Ĺ����ų������������DZ��е�һ����a1��a2��a4��a7�������ɵ�����Ϊ{bn}��b1=a1=1��SnΪ����{bn}��ǰn��ͣ�������2bn=bnSn-Sn2��n��2��n��N*����
������{an}�е������ÿһ�б���һ�ж�һ��Ĺ����ų������������DZ��е�һ����a1��a2��a4��a7�������ɵ�����Ϊ{bn}��b1=a1=1��SnΪ����{bn}��ǰn��ͣ�������2bn=bnSn-Sn2��n��2��n��N*���� ������{an}�е������ÿһ�б���һ�ж�һ��Ĺ����ų����±���
������{an}�е������ÿһ�б���һ�ж�һ��Ĺ����ų����±���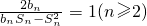 ��
��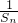 �ɵȲ����У���������{bn}��ͨ�ʽ��
�ɵȲ����У���������{bn}��ͨ�ʽ��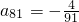 ʱ������q��ֵ��
ʱ������q��ֵ��
 ��bΪ���ڵ���3������������������{cn}���Ƿ������������ɵȱ����У������ڣ�������гɵȱ����е���������������ڣ���˵�����ɣ�
��bΪ���ڵ���3������������������{cn}���Ƿ������������ɵȱ����У������ڣ�������гɵȱ����е���������������ڣ���˵�����ɣ�