练习册

  • 练习册
  • 试题
    精英家教网 > 高中数学 > 题目详情
    2．某射手射击一次，命中环数与概率如表：
    命中环数  10环  9环  8环  7环7环以下
      概率0.160.320.240.200.08
    计算：
    （1）射击一次，命中环数不低于7环的概率．
    （2）射击一次，至少命中8环的概率．

    分析 （1）记“命中环数不低于7环”为事件A，由概率分布表能求出可得命中环数不低于7环的概率．
    （2）记“至少命中8环”为事件B，由概率分布表能求出至少命中8环的概率．

    解答 解：（1）记“命中环数不低于7环”为事件A，
    则由上表可得其概率P（A）=1-0.08=0.92．（5分）
    （或者P（A）=0.16+0.32+0.24+0.20=0.92）
    （2）记“至少命中8环”为事件B，
    则由上表可得其概率：
    P（B）=0.16+0.32+0.24=0.72．（5分）

    点评 本题考查概率的求法，是基础题，解题时要认真审题，注意对立事件概率计算公式的合理运用．

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：高中数学 来源： 题型：选择题

    12．若函数f（x）=cos$\frac{x+2φ}{3}$（φ∈[-π，0]）是奇函数，则下列说法错误的是（　　）
    A．f（-1-6π）+f（1+12π）=0
    B．函数f（x）的一个单调递减区间为[$\frac{17π}{2}$，10π]
    C．函数f（x）的一个对称中心为（3π，0）
    D．函数g（x）=f（6x）-$\frac{1}{2}$在[0，9]上有4个零点

    查看答案和解析>>

    科目：高中数学 来源： 题型：填空题

    13．曲线y=ex在点x=0处的切线的倾斜角为$\frac{π}{4}$．

    查看答案和解析>>

    科目：高中数学 来源： 题型：解答题

    10．已知定义在R上的函数f（x）满足：
    ①f（1）=2； ②当x＞0时，f（x）＞1； ③对任意的x，y∈R，都有f（x+y）=f（x）•f（y）．
    （1）求证：f（0）=1，且对任意x＜0时，0＜f（x）＜1；
    （2）求证：f（x）在R上是单调递增函数；
    （3）求满足f（3x-x2）＞4的所有x的值．

    查看答案和解析>>

    科目：高中数学 来源： 题型：选择题

    17．下列程序运行后的结果为（　　）
    A．0B．-4C．2D．-2

    查看答案和解析>>

    科目：高中数学 来源： 题型：选择题

    7．关于x的方程$\sqrt{1-{x^2}}+a=x$有两个不相等实数根，则实数a的取值范围是（　　）
    A．$（1，\sqrt{2}]$B．$（-1，\sqrt{2}]$C．$（-\sqrt{2}，-1]$D．$（-\sqrt{2}，1]$

    查看答案和解析>>

    科目：高中数学 来源： 题型：解答题

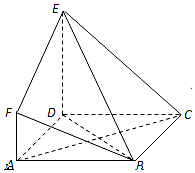    14．如图，四边形ABCD是边长为2的正方形，DE⊥平面ABCD，AF∥DE，DE=2AF，∠EBD=45°．
    （Ⅰ）求证：AC⊥平面BDE；
    （Ⅱ）求该几何体的体积．

    查看答案和解析>>

    科目：高中数学 来源： 题型：解答题

    11．在平面直角坐标系xoy中，直线l经过点P（-3，0），其倾斜角为α，以原点O为极点，以x轴非负半轴为极轴，与直角坐标系xoy取相同的长度单位，建立极坐标系．设曲线C的极坐标方程为ρ2-2ρcosθ-3=0．
    （1）若直线l与曲线C有公共点，求倾斜角α的取值范围；
    （2）设M（x，y）为曲线C上任意一点，求x+y的取值范围．

    查看答案和解析>>

    科目：高中数学 来源： 题型：选择题

    12．同时具备以下性质：（1）最小正周期为π；（2）图象关于x=$\frac{π}{3}$对称；（3）在[-$\frac{π}{6}$，$\frac{π}{3}$]上是增函数的是（　　）
    A．y=sin（$\frac{x}{2}$+$\frac{π}{6}$）B．y=cos（2x+$\frac{π}{3}$）C．y=sin（2x-$\frac{π}{6}$）D．y=cos（2x-$\frac{π}{6}$）

    查看答案和解析>>

    同步练习册答案