
【题目】已知A、F分别是椭圆C: ![]() +
+ ![]() =1(a>b>0)的左顶点、右焦点,点P为椭圆C上一动点,当PF⊥x轴时,AF=2PF.
=1(a>b>0)的左顶点、右焦点,点P为椭圆C上一动点,当PF⊥x轴时,AF=2PF.
(1)求椭圆C的离心率;
(2)若椭圆C存在点Q,使得四边形AOPQ是平行四边形(点P在第一象限),求直线AP与OQ的斜率之积;
(3)记圆O:x2+y2= ![]() 为椭圆C的“关联圆”.若b=
为椭圆C的“关联圆”.若b= ![]() ,过点P作椭圆C的“关联圆”的两条切线,切点为M、N,直线MN的横、纵截距分别为m、n,求证:
,过点P作椭圆C的“关联圆”的两条切线,切点为M、N,直线MN的横、纵截距分别为m、n,求证: ![]() +
+ ![]() 为定值.
为定值.
【答案】
(1)
解:由PF⊥x轴,知xP=c,代入椭圆C的方程,
得: ![]() +
+ ![]() =1,解得
=1,解得 ![]() ,
,
又AF=2PF,∴a+c= ![]() ,
,
∴a2+ac=2b2,即a2﹣2c2﹣ac=0,
∴2e2+e﹣1=0,
由e>0解得椭圆C的离心率e= ![]() .
.
(2)
解:∵四边形AOPQ是平行四边形,∴PQ=a,且PF∥x轴,
∴ ![]() ,代入椭圆C的方程,解得
,代入椭圆C的方程,解得 ![]() ,
,
∵点P在第一象限,∴yp= ![]() b,
b,
同理可得xQ=﹣ ![]() ,yQ=
,yQ= ![]() b,
b,
∴kAPkOQ= ![]()
![]() =﹣
=﹣ ![]() ,
,
由(1)知e= ![]() ,得
,得 ![]() =
= ![]() ,∴kAPkOQ=﹣
,∴kAPkOQ=﹣ ![]() .
.
(3)
证明:由(1)知e= ![]() =
= ![]() ,又b=
,又b= ![]() ,解得a=2,
,解得a=2,
∴椭圆C的方程为 ![]() =1,
=1,
圆O的方程为x2+y2= ![]() ,①…
,①…
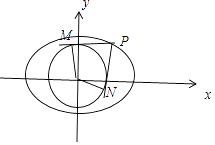
连接OM,ON,由题意可知,OM⊥PM,ON⊥PN,
∴四边形OMPN的外接圆是以OP 为直径的圆,
设P(x0,y0),则四边形OMPN的外接圆方程为(x﹣ ![]() )2+(y﹣
)2+(y﹣ ![]() )2=
)2= ![]() (
( ![]() ),
),
即 ![]() =0,②…
=0,②…
①﹣②,得直线MN的方程为xx0+yy0= ![]() ,
,
令y=0,则m= ![]() ,令x=0,则n=
,令x=0,则n= ![]() .
.
∴ ![]() +
+ ![]() =49(
=49( ![]() ),
),
∵点P在椭圆C上,∴ ![]() +
+ ![]() =1,
=1,
∴ ![]() =49(为定值).…
=49(为定值).…
【解析】(1)由PF⊥x轴,知xP=c,代入椭圆C的方程,得 ![]() ,由此能求出椭圆C的离心率.(2)由四边形AOPQ是平行四边形,知PQ=a,且PF∥x轴,从而yp=
,由此能求出椭圆C的离心率.(2)由四边形AOPQ是平行四边形,知PQ=a,且PF∥x轴,从而yp= ![]() b,yQ=
b,yQ= ![]() b,由此能求出kAPkOQ . (3)由(1)知e=
b,由此能求出kAPkOQ . (3)由(1)知e= ![]() =
= ![]() ,又b=
,又b= ![]() ,从而椭圆C的方程为
,从而椭圆C的方程为 ![]() =1,圆O的方程为x2+y2=
=1,圆O的方程为x2+y2= ![]() ,连接OM,ON,由题意可知,OM⊥PM,ON⊥PN,从而四边形OMPN的外接圆是以OP 为直径的圆,由此能证明
,连接OM,ON,由题意可知,OM⊥PM,ON⊥PN,从而四边形OMPN的外接圆是以OP 为直径的圆,由此能证明 ![]() 为定值.
为定值.
【考点精析】本题主要考查了椭圆的标准方程的相关知识点,需要掌握椭圆标准方程焦点在x轴:![]() ,焦点在y轴:
,焦点在y轴:![]() 才能正确解答此题.
才能正确解答此题.


 第1卷单元月考期中期末系列答案
第1卷单元月考期中期末系列答案科目:高中数学 来源: 题型:
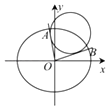
【题目】如图所示,已知椭圆C: ![]() +
+ ![]() =1(a>b>0)的焦距为2,直线y=x被椭圆C截得的弦长为
=1(a>b>0)的焦距为2,直线y=x被椭圆C截得的弦长为 ![]() .
.
(Ⅰ)求椭圆C的方程;
(Ⅱ)设点M(x0 , y0)是椭圆C上的动点,过原点O引两条射线l1 , l2与圆M:(x﹣x0)2+(y﹣y0)2= ![]() 分别相切,且l1 , l2的斜率k1 , k2存在.
分别相切,且l1 , l2的斜率k1 , k2存在.
①试问k1k2是否定值?若是,求出该定值,若不是,说明理由;
②若射线l1 , l2与椭圆C分别交于点A,B,求|OA||OB|的最大值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数f(x)=x2﹣x,g(x)=ex﹣ax﹣1(e为自然对数的底数).
(1)讨论函数g(x)的单调性;
(2)当x>0时,f(x)≤g(x)恒成立,求实数a的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,在四棱柱ABCD﹣A1B1C1D1中,平面A1ABB1⊥底面ABCD,且∠ABC= ![]() .
. 
(1)求证:B1C1∥平面BCD1;
(2)求证:平面A1ABB1⊥平面BCD1 .
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】合肥一中、六中为了加强交流,增进友谊,两校准备举行一场足球赛,由合肥一中版画社的同学设计一幅矩形宣传画,要求画面面积为![]() ,画面的上、下各留
,画面的上、下各留![]() 空白,左、右各留
空白,左、右各留![]() 空白.
空白.

(1)如何设计画面的高与宽的尺寸,才能使宣传画所用纸张面积最小?
(2)设画面的高与宽的比为![]() ,且
,且![]() ,求
,求![]() 为何值时,宣传画所用纸张面积最小?
为何值时,宣传画所用纸张面积最小?
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】设函数f(x)=xex﹣ax2(a∈R).
(1)若函数g(x)= ![]() 是奇函数,求实数a的值;
是奇函数,求实数a的值;
(2)若对任意的实数a,函数h(x)=kx+b(k,b为实常数)的图象与函数f(x)的图象总相切于一个定点. ①求k与b的值;
②对(0,+∞)上的任意实数x1 , x2 , 都有[f(x1)﹣h(x1)][f(x2)﹣h(x2)]>0,求实数a的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】一只袋中装有编号为1,2,3,…,n的n个小球,n≥4,这些小球除编号以外无任何区别,现从袋中不重复地随机取出4个小球,记取得的4个小球的最大编号与最小编号的差的绝对值为ξn , 如ξ4=3,ξ5=3或4,ξ6=3或4或5,记ξn的数学期望为f(n).
(1)求f(5),f(6);
(2)求f(n).
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】设不等式﹣2<|x﹣1|﹣|x+2|<0的解集为M,a、b∈M,
(1)证明:| ![]() a+
a+ ![]() b|<
b|< ![]() ;
;
(2)比较|1﹣4ab|与2|a﹣b|的大小,并说明理由.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com