
已知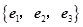 为空间的一个基底,且
为空间的一个基底,且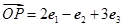 ,
,
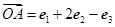 ,
,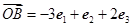 ,
,
(1)判断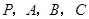 四点是否共面;
四点是否共面;
(2)能否以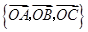 作为空间的一个基底?若不能,说明理由;若能,试以这一基底表示向量
作为空间的一个基底?若不能,说明理由;若能,试以这一基底表示向量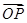
(1)四点不共面; (2) .
.
【解析】本试题主要是考查了空间向量中四点共面的问题,以及判定空间向量的基底的定义的运用。
(1)假设四点共面,则存在实数 使
使 ,
,
且 ,那么可以根据这个结论得到方程组,求解判定不成立。
,那么可以根据这个结论得到方程组,求解判定不成立。
(2)利用不同面的三个向量可以充当空间的基底,那么我们可以得到,判定
解:(1)假设四点共面,则存在实数 使
使 ,
,
且 ,
,
即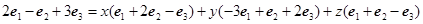 .…4分
.…4分
比较对应的系数,得一关于 的方程组
的方程组
解得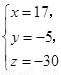
与 矛盾,故四点不共面;……………6分
矛盾,故四点不共面;……………6分
(2)若向量 ,
, ,
, 共面,则存在实数
共面,则存在实数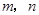 使
使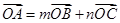 ,
,
同(1)可证,这不可能,
因此 可以作为空间的一个基底,
可以作为空间的一个基底,
令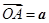 ,
, ,
, ,
,
由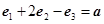 ,
, ,
, 联立得到方程组,
联立得到方程组,
从中解得 ………………10分所以
………………10分所以


 培优好卷单元加期末卷系列答案
培优好卷单元加期末卷系列答案科目:高中数学 来源: 题型:
| OP |
| OA |
| OB |
| OC |
| OA |
| OB |
| OC |
| OP |
查看答案和解析>>
科目:高中数学 来源: 题型:单选题
 ,则
,则 ;
; 不构成空间的一个基底,则A、B、M、N共面;
不构成空间的一个基底,则A、B、M、N共面; ,则
,则 与任何向量不构成空间的一个基底;
与任何向量不构成空间的一个基底;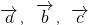 是空间的一个基底,则基向量
是空间的一个基底,则基向量 可以与向量
可以与向量 构成空间另一个基底.
构成空间另一个基底.查看答案和解析>>
科目:高中数学 来源:《第3章 空间向量与立体几何》2009年单元测试卷(东升学校)(解析版) 题型:选择题
 ,则
,则 ;
; 不构成空间的一个基底,则A、B、M、N共面;
不构成空间的一个基底,则A、B、M、N共面; ,则
,则 与任何向量不构成空间的一个基底;
与任何向量不构成空间的一个基底; 是空间的一个基底,则基向量
是空间的一个基底,则基向量 可以与向量
可以与向量 构成空间另一个基底.
构成空间另一个基底.查看答案和解析>>
科目:高中数学 来源:2009-2010学年度新课标高三上学期数学单元测试8-理科-立体几何初步、空间向量与立体几何 题型:解答题
已知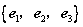 为空间的一个基底,且
为空间的一个基底,且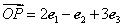 ,
,
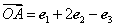 ,
,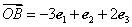 ,
,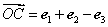 .
.
(1)判断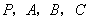 四点是否共面;
四点是否共面;
(2)能否以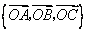 作为空间的一个基底?若不能,说明理由;若能,试以这一基底表示向量
作为空间的一个基底?若不能,说明理由;若能,试以这一基底表示向量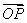 .
.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com