
【题目】已知函数![]() ,
, ![]() ,其中
,其中![]() 是
是![]() 的导函数.
的导函数.
(Ⅰ)求曲线![]() 在点
在点![]() 处的切线方程;
处的切线方程;
(Ⅱ)若![]() 在
在![]() 上恒成立,求实数
上恒成立,求实数![]() 的取值范围.
的取值范围.
【答案】(Ⅰ)![]() ;(Ⅱ)
;(Ⅱ)![]() .
.
【解析】试题分析:(Ⅰ) ![]() ,切线的斜率
,切线的斜率![]() ,所以切线方程为
,所以切线方程为![]() ,即
,即![]() .
.
(Ⅱ)![]() 在
在![]() 上恒成立,即
上恒成立,即![]() 在
在![]() 上恒成立,即
上恒成立,即![]() ,构造
,构造![]() 求最小值即可.
求最小值即可.
试题解析:
(Ⅰ)函数![]() 的定义域为
的定义域为![]() ,且
,且![]() ,
,
由导数的几何意义所求切线的斜率![]() ,
,
所以所求的切线方程为![]() ,即
,即![]() .
.
(Ⅱ)![]() ,
, ![]() ,
,
∴![]() 在
在![]() 上恒成立,
上恒成立,
即![]() ,即
,即![]() 在
在![]() 上恒成立,即
上恒成立,即![]() .
.
令![]() ,则
,则 ,
,
令![]() ,
, ![]() ,
,
当![]() 时,
时, ![]() ,∴
,∴![]() 在
在![]() 上单调递增.
上单调递增.
∴![]() ,∴
,∴![]() (
(![]() ),
),
∴![]() ,∴
,∴![]() 在
在![]() 上单调递增,当然在
上单调递增,当然在![]() 上也单调递增,
上也单调递增,
∴![]() ,
,
∴![]() .
.
点晴:本题主要考查导数与切线,导数与极值点、不等式等知识. 解答此类问题,应该首先确定函数的定义域,否则,写出的单调区间易出错. 解决含参数问题及不等式问题注意两个转化:(1)利用导数解决含有参数的单调性问题可将问题转化为不等式恒成立问题,要注意分类讨论和数形结合思想的应用.(2)将不等式的证明、方程根的个数的判定转化为函数的单调性,最值问题处理.


 快捷英语周周练系列答案
快捷英语周周练系列答案科目:高中数学 来源: 题型:
【题目】下面几种推理过程是演绎推理的是 ( )
A. 某校高三(1)班有55人,2班有54人,3班有52人,由此得高三所有班人数超过50人
B. 两条直线平行,同旁内角互补,如果∠A与∠B是两条平行直线的同旁内角,则∠A+∠B=180°
C. 由平面三角形的性质,推测空间四边形的性质
D. 在数列{an}中,a1=1,an=![]() (an-1+
(an-1+![]() )(n≥2),由此归纳出{an}的通项公
)(n≥2),由此归纳出{an}的通项公
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知☉O:x2+y2=1和定点A(2,1),由☉O外一点P(a,b)向☉O引切线PQ,切点为Q,且满足|PQ|=|PA|.
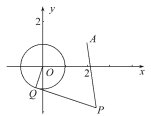
(1)求实数a,b间满足的等量关系.
(2)求线段PQ长的最小值.
(3)若以P为圆心所作的☉P与☉O有公共点,试求半径取最小值时☉P的方程.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知长方形![]() ,
, ![]() ,
, ![]() ,以
,以![]() 的中点
的中点![]() 为原点,建立如图所示的平面直角坐标系
为原点,建立如图所示的平面直角坐标系![]() .
.
(1)求以![]() 为焦点,且过
为焦点,且过![]() 两点的椭圆的标准方程;
两点的椭圆的标准方程;
(2)在(1)的条件下,过点![]() 作直线
作直线![]() 与椭圆交于不同的两点
与椭圆交于不同的两点![]() ,设
,设![]() ,点
,点![]() 坐标为
坐标为![]() ,若
,若![]() ,求
,求![]() 的取值范围.
的取值范围.

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com