
【题目】要了解全校学生的体重情况,请你设计一个调查方案,并实施调查,完成一份统计调查分析报告
【答案】答案见解析
【解析】
根据年级的不同,对不同年级的学生进行分层抽样;对同一年级的学生,按照系统抽样的方法抽样.将所得样本做出频率分布表,进而作频率分布直方图.通过频率分布直方图,计算所有学生体重的平均数、众数和中位数,可以估计全校学生的体重情况.
设全校共有3600人.高一年级有学生1200人,学号编号依次为![]() ;高二年级有学生1200人,学号编号依次为
;高二年级有学生1200人,学号编号依次为![]() ;高三年级有学生1200人,学号编号依次为
;高三年级有学生1200人,学号编号依次为![]() .
.
在全校中抽取120人的样本.按照年级分层抽样,每个年级抽取40人.每个年级按照学号进行系统抽样,所得120个学生体重的数据如下所示(体重取整数kg):
57,53,44,61,56, 48,63,59,44,62,
56,69,42,71,64, 70,38,74,45,59,
46,72,50,63,51, 78,43,70,57,65,
44,49,63,52,72, 67,69,56,67,62,
55,76,63,65,58, 60,78,63,76,58.
58,61,59,71,64, 66,58,73,56,67.
55,67,40,62,46, 41,62,58,74,64,
53,45,67,49,65, 71,40,44,56,47,
56,45,55,57,71, 64,39,69,44,39,
53,48,60,58,64, 70,61,49,55,58,
64,45,48,52,67, 58,72,66,73,54.
64,48,40,56,47, 64,62,70,77,68.
由以上数据可知,体重最轻的为38 kg,体重最重的为78 kg .极差为40 kg
所以将数据分为8组,组距为5.
频率分布表如下图所示:
分组 | 频数 | 频率 |
|
| 9 | 0.075 | 0.015 |
| 12 | 0.1 | 0.02 |
| 12 | 0.1 | 0.02 |
| 18 | 0.15 | 0.03 |
| 21 | 0.175 | 0.035 |
| 24 | 0.2 | 0.04 |
| 15 | 0.125 | 0.025 |
| 9 | 0.075 | 0.015 |
总计 | 120 | 1 | 0.2 |
由评率分布表,可得频率分布直方图如下图所示:

通过频率分布直方图,可得样本的平均体重为![]()
![]() kg
kg
众数为![]() kg
kg
中位数为![]() kg
kg
根据样本数据分析可知,全校学生的平均体重约为![]() kg,体重的中位数约为60 kg,体重的众数为63.5 kg.
kg,体重的中位数约为60 kg,体重的众数为63.5 kg.


 开心试卷期末冲刺100分系列答案
开心试卷期末冲刺100分系列答案 双基同步导航训练系列答案
双基同步导航训练系列答案科目:高中数学 来源: 题型:
【题目】2019年4月26日,铁人中学举行了盛大的成人礼.仪式在《相信我们会创造奇迹》的歌声中拉开序幕,庄严而神圣的仪式感动了无数家长,4月27日,铁人中学官方微信发布了整个仪式精彩过程,几十年众志成城,数十载砥砺奋进,铁人中学正在创造着一个又一个奇迹.官方微信发布后,短短几个小时点击量就突破了万人,收到了非常多的精彩留言.学校从众多留言者中抽取了100人参加“学校满意度调查”,其留言者年龄集中在![]() 之间,根据统计结果,做出频率分布直方图如下:
之间,根据统计结果,做出频率分布直方图如下:

(Ⅰ)求这100位留言者年龄的样本平均数![]() 和样本方差
和样本方差![]() (同一组数据用该区间的中点值作代表);
(同一组数据用该区间的中点值作代表);
(Ⅱ)由频率分布直方图可以认为,留言者年龄![]() 服从正态分布
服从正态分布![]() ,其中
,其中![]() 近似为样本均数
近似为样本均数![]() ,
,![]() 近似为样本方差
近似为样本方差![]() .
.
(ⅰ)利用该正态分布,求![]() ;
;
(ii)学校从年龄在![]() 和
和![]() 的留言者中,按照分层抽样的方法,抽出了7人参加“精彩留言”表彰大会,现要从中选出3人作为代表发言,设这3位发言者的年龄落在区间
的留言者中,按照分层抽样的方法,抽出了7人参加“精彩留言”表彰大会,现要从中选出3人作为代表发言,设这3位发言者的年龄落在区间![]() 的人数是
的人数是![]() ,求变量
,求变量![]() 的分布列和数学期望.附:
的分布列和数学期望.附:![]() ,若
,若![]() ,则
,则![]() ,
,![]() .
.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】上饶某中学一研究性学习小组早晨在校门口询问调查同学的体重,对来校同学依次每5人抽取一人询问体重,共抽取40位同学,将他们的体重(![]() 分成六段:
分成六段:![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,统计后得到如图的频率分布直方图.
,统计后得到如图的频率分布直方图.
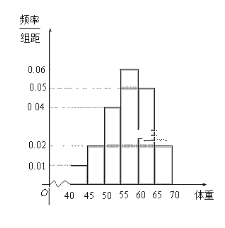
(1)此研究性学习小组在采样中,用到的是什么抽样方法?并求这40位同学体重的众数和中位数的估计值.
(2)从体重在![]() 的同学中任意抽取3位,求体重在
的同学中任意抽取3位,求体重在![]() ,
,![]() 内都有同学的概率.
内都有同学的概率.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在四棱锥![]() 中,
中, ![]() 平面
平面![]() ,
, ![]() ,
, ![]() ,
, ![]() ,
, ![]() ,
, ![]() ,
, ![]() 是
是![]() 的中点,
的中点, ![]() 在线段
在线段![]() 上,且满足
上,且满足![]() .
.

(1)求证: ![]() 平面
平面![]() ;
;
(2)求二面角![]() 的余弦值;
的余弦值;
(3)在线段![]() 上是否存在点
上是否存在点![]() ,使得
,使得![]() 与平面
与平面![]() 所成角的余弦值是
所成角的余弦值是![]() ,若存在,求出
,若存在,求出![]() 的长;若不存在,请说明理由.
的长;若不存在,请说明理由.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某校高三年级数学竞赛初赛考试后,对90分以上(含90分)的成绩进行统计,其频率分布直方图如图所示,已知成绩在130~140分数段的人数为2.
(1)求这组数据的平均数M.
(2)现根据初赛成绩从第一组和第五组(从低分段至高分段依次为第一组、第二组、…、第五组)中任意选出两人,形成帮扶小组.若选出的两人的成绩之差大于20,则称这两人为“黄金搭档组”,试求选出的两人为“黄金搭档组”的概率.

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com