
分析 先求出a6=-2,从$\frac{4}{{{a_1}{a_7}}}$+$\frac{8}{{{a_2}{a_{10}}}}$+$\frac{16}{{{a_4}{a_{12}}}}$=$\frac{4}{{{a}_{4}}^{2}}$+$\frac{8}{{{a}_{6}}^{2}}$+$\frac{16}{{{a}_{8}}^{2}}$=$\frac{4}{(\frac{-2}{{q}^{2}})^{2}}$+2+$\frac{16}{(-2{q}^{2})^{2}}$,由此利用基本不等式性质能求出$\frac{4}{{{a_1}{a_7}}}$+$\frac{8}{{{a_2}{a_{10}}}}$+$\frac{16}{{{a_4}{a_{12}}}}$的最小值.
解答 解:∵数列{an}是等比数列,a3a6a9=${{a}_{6}}^{3}$=-8,
∴a6=-2
∴$\frac{4}{{{a_1}{a_7}}}$+$\frac{8}{{{a_2}{a_{10}}}}$+$\frac{16}{{{a_4}{a_{12}}}}$
=$\frac{4}{{{a}_{4}}^{2}}$+$\frac{8}{{{a}_{6}}^{2}}$+$\frac{16}{{{a}_{8}}^{2}}$
=$\frac{4}{(\frac{-2}{{q}^{2}})^{2}}$+2+$\frac{16}{(-2{q}^{2})^{2}}$
=${q}^{4}+\frac{4}{{q}^{4}}$+2
$≥2\sqrt{{q}^{4}×\frac{4}{{q}^{4}}}$+2=6.
当且仅当${q}^{4}=\frac{4}{{q}^{4}}$时取等号,
∴$\frac{4}{{{a_1}{a_7}}}$+$\frac{8}{{{a_2}{a_{10}}}}$+$\frac{16}{{{a_4}{a_{12}}}}$的最小值为6.
故答案为:6.
点评 本题考查代数式的最小值的求法,是中档题,解题时要认真审题,注意等差数列的性质、基本不等式性质的合理运用.


 探究与巩固河南科学技术出版社系列答案
探究与巩固河南科学技术出版社系列答案科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
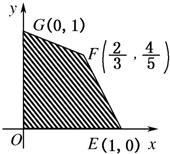 如图,目标函数z=kx-y的可行域为四边形OEFG(含边界),若点F($\frac{2}{3}$,$\frac{4}{5}$)是目标函数的最优解,则k的取值范围是( )
如图,目标函数z=kx-y的可行域为四边形OEFG(含边界),若点F($\frac{2}{3}$,$\frac{4}{5}$)是目标函数的最优解,则k的取值范围是( )| A. | (-$\frac{12}{5}$,$\frac{4}{5}$) | B. | ($\frac{3}{10},\frac{12}{5}$) | C. | [-$\frac{12}{5}$,-$\frac{3}{10}$] | D. | [-$\frac{3}{10}$,-$\frac{12}{5}$] |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | (-1,-2,1) | B. | (-1,2,1) | C. | (1,-2,-1) | D. | (1,2,-1) |
查看答案和解析>>
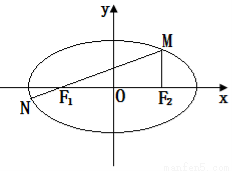
科目:高中数学 来源:2015-2016学年江苏泰兴中学高二上学期期末数学(文)试卷(解析版) 题型:解答题
设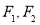 分别是椭圆
分别是椭圆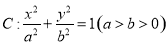 的左右焦点,
的左右焦点,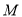 是
是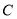 上一点,且
上一点,且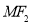 与
与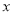 轴垂直,直线
轴垂直,直线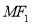 与
与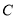 的另一个交点为
的另一个交点为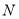 .
.
(1)若直线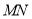 的斜率为
的斜率为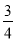 ,求
,求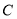 的离心率;
的离心率;
(2)若直线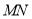 在
在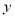 轴上的截距为2,且
轴上的截距为2,且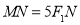 ,求椭圆
,求椭圆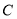 的方程.
的方程.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com