
【题目】已知抛物线E∶y2=2px(p>0)的焦点为F,过F且斜率为1的直线交E于A,B两点,线段AB的中点为M,其垂直平分线交x轴于点C,MN⊥y轴于点N.若四边形CMNF的面积等于7,则E的方程为( )
A.y2=xB.y2=2x
C.y2=4xD.y2=8x
科目:高中数学 来源: 题型:
【题目】下列问题中,![]() 是不相等的正数,比较
是不相等的正数,比较![]() 的表达式,下列选项正确的是( )
的表达式,下列选项正确的是( )
问题甲:一个直径![]() 寸的披萨和一个直径
寸的披萨和一个直径![]() 寸的披萨,面积和等于两个直径都是
寸的披萨,面积和等于两个直径都是![]() 寸的披萨;
寸的披萨;
问题乙:某人散步,第一圈的速度是![]() ,第二圈的速度是
,第二圈的速度是![]() ,这两圈的平均速度为
,这两圈的平均速度为![]() ;
;
问题丙:将一物体放在两臂不等长的天平测量,放在左边时砝码质量为![]() (天平平衡),放在右边时左边砝码质量为
(天平平衡),放在右边时左边砝码质量为![]() ,物体的实际质量为
,物体的实际质量为![]() .
.
A.![]() B.
B.![]() C.
C.![]() D.
D.![]() 互不相同
互不相同
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知抛物线C; y2 =2x的焦点为F,准线为l, P为抛物线C上异于顶点的动点.
(1)过点P作准线1的垂线,垂足为H,若△PHF与△POF的面积之比为2:1,求点P的坐标;
(2)过点M(![]() ,0)任作一条直线 m与抛物线C交于不同的两点A, B.若两直线PA, PB 斜率之和为2,求点P的坐标.
,0)任作一条直线 m与抛物线C交于不同的两点A, B.若两直线PA, PB 斜率之和为2,求点P的坐标.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图所示,![]() 是某海湾旅游区的一角,其中
是某海湾旅游区的一角,其中![]() ,为了营造更加优美的旅游环境,旅游区管委会决定在直线海岸
,为了营造更加优美的旅游环境,旅游区管委会决定在直线海岸![]() 和
和![]() 上分别修建观光长廊
上分别修建观光长廊![]() 和AC,其中
和AC,其中![]() 是宽长廊,造价是
是宽长廊,造价是![]() 元/米,
元/米,![]() 是窄长廊,造价是
是窄长廊,造价是![]() 元/米,两段长廊的总造价为120万元,同时在线段
元/米,两段长廊的总造价为120万元,同时在线段![]() 上靠近点
上靠近点![]() 的三等分点
的三等分点![]() 处建一个观光平台,并建水上直线通道
处建一个观光平台,并建水上直线通道![]() (平台大小忽略不计),水上通道的造价是
(平台大小忽略不计),水上通道的造价是![]() 元/米.
元/米.
(1) 若规划在三角形![]() 区域内开发水上游乐项目,要求
区域内开发水上游乐项目,要求![]() 的面积最大,那么
的面积最大,那么![]() 和
和![]() 的长度分别为多少米?
的长度分别为多少米?
(2) 在(1)的条件下,建直线通道![]() 还需要多少钱?
还需要多少钱?

查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】设S、T是R的两个非空子集,如果函数![]() 满足:①
满足:①![]() ;②对任意
;②对任意![]() ,
,![]() ,当
,当![]() 时,恒有
时,恒有![]() ,那么称函数
,那么称函数![]() 为集合S到集合T的“保序同构函数”.
为集合S到集合T的“保序同构函数”.
(1)试写出集合![]() 到集合R的一个“保序同构函数”;
到集合R的一个“保序同构函数”;
(2)求证:不存在从集合Z到集合Q的“保序同构函数”;
(3)已知![]() 是集合
是集合![]() 到集合
到集合![]() 的“保序同构函数”,求s和t的最大值.
的“保序同构函数”,求s和t的最大值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】各项均为正数的数列{an}的首项![]() ,前n项和为Sn,且Sn+1+Sn=λ
,前n项和为Sn,且Sn+1+Sn=λ![]() ..
..
(1)求{an}的通项公式;
(2)若数列{bn}满足bn=λnan,求{bn}的前n项和Tn.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在中国足球超级联赛某一季的收官阶段中,广州恒大淘宝、北京中赫国安、上海上港、山东鲁能泰山分别积分59分、58分、56分、50分,四家俱乐部都有机会夺冠.A,B,C三个球迷依据四支球队之前比赛中的表现,结合自已的判断,对本次联赛的冠军进行如下猜测:![]() 猜测冠军是北京中赫国安或山东鲁能泰山;
猜测冠军是北京中赫国安或山东鲁能泰山;![]() 猜测冠军一定不是上海上港和山东鲁能泰山;
猜测冠军一定不是上海上港和山东鲁能泰山;![]() 猜测冠军是广州恒大淘宝或北京中赫国安.联赛结束后,发现A,B,C三人中只有一人的猜测是正确的,则冠军是( )
猜测冠军是广州恒大淘宝或北京中赫国安.联赛结束后,发现A,B,C三人中只有一人的猜测是正确的,则冠军是( )
A.广州恒大淘宝B.北京中赫国安C.上海上港D.山东鲁能泰山
查看答案和解析>>
科目:高中数学 来源: 题型:
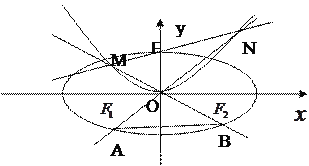
【题目】如图,椭圆![]()
![]() 的左右焦点分别为的
的左右焦点分别为的![]() 、
、![]() ,离心率为
,离心率为![]() ;过抛物线
;过抛物线![]() 焦点
焦点![]() 的直线交抛物线于
的直线交抛物线于![]() 、
、![]() 两点,当
两点,当![]() 时,
时, ![]() 点在
点在![]() 轴上的射影为
轴上的射影为![]() 。连结
。连结![]() 并延长分别交
并延长分别交![]() 于
于![]() 、
、![]() 两点,连接
两点,连接![]() ;
; ![]() 与
与![]() 的面积分别记为
的面积分别记为![]() ,
, ![]() ,设
,设![]() .
.
(Ⅰ)求椭圆![]() 和抛物线
和抛物线![]() 的方程;
的方程;
(Ⅱ)求![]() 的取值范围.
的取值范围.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com