
【题目】甲、乙等五名奥运志愿者被随机地分到A,B,C,D四个不同的岗位服务,每个岗位至少有一名志愿者.
(1)求甲、乙两人同时参加A岗位服务的概率;
(2)求甲、乙两人不在同一个岗位服务的概率;
(3)设随机变量ξ为这五名志愿者中参加A岗位服务的人数,求ξ的分布列.
【答案】
(1)解:记甲、乙两人同时参加A岗位服务为事件EA,
总事件数是从5个人中选2个作为一组,同其他3人共4个元素在四个位置进行排列C52A44.
满足条件的事件数是A33,
那么 ![]() ,
,
即甲、乙两人同时参加A岗位服务的概率是 ![]() .
.
(2)解:记甲、乙两人同时参加同一岗位服务为事件E,
满足条件的事件数是A44,
那么 ![]() ,
,
∴甲、乙两人不在同一岗位服务的概率是 ![]() .
.
(3)解:随机变量ξ可能取的值为1,2.事件“ξ=2”是指有两人同时参加A岗位服务,
则 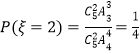 .
.
∴ ![]() ,ξ的分布列是
,ξ的分布列是
ξ | 1 | 2 |
P |
|
|
【解析】(1)甲、乙两人同时参加A岗位服务,则另外三个人在B、C、D三个位置进行全排列,所有的事件数是从5个人中选2个作为一组,同其他3人共4个元素在四个位置进行排列.(2)总事件数同第一问一样,甲、乙两人不在同一个岗位服务的对立事件是甲、乙两人同时参加同一岗位服务,即甲、乙两人作为一个元素同其他三个元素进行全排列.(3)五名志愿者中参加A岗位服务的人数ξ可能的取值是1、2,ξ=2”是指有两人同时参加A岗位服务,同第一问类似做出结果.写出分布列.
【考点精析】利用离散型随机变量及其分布列对题目进行判断即可得到答案,需要熟知在射击、产品检验等例子中,对于随机变量X可能取的值,我们可以按一定次序一一列出,这样的随机变量叫做离散型随机变量.离散型随机变量的分布列:一般的,设离散型随机变量X可能取的值为x1,x2,.....,xi,......,xn,X取每一个值 xi(i=1,2,......)的概率P(ξ=xi)=Pi,则称表为离散型随机变量X 的概率分布,简称分布列.


科目:高中数学 来源: 题型:
【题目】已知数列{an}中,a1=1,前n项和Sn= ![]() an .
an .
(1)求a2 , a3 , 及{an}的通项公式.
(2)求{ ![]() }的前n项和Tn , 并证明:1≤Tn<2.
}的前n项和Tn , 并证明:1≤Tn<2.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知数列![]() ,其前
,其前![]() 项和为
项和为![]() .
.
(1)若对任意的![]() ,
, ![]() ,
, ![]() ,
, ![]() 组成公差为4的等差数列,且
组成公差为4的等差数列,且![]() ,求
,求![]() ;
;
(2)若数列 是公比为
是公比为![]() (
(![]() )的等比数列,
)的等比数列, ![]() 为常数,
为常数,
求证:数列![]() 为等比数列的充要条件为
为等比数列的充要条件为![]() .
.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】抛物线C:y2=2x的准线方程是 , 经过点P(4,1)的直线l与抛物线C相交于A,B两点,且点P恰为AB的中点,F为抛物线的焦点,则 ![]() = .
= .
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数f(x)=x|2x﹣a|,g(x)= ![]() (a∈R),若0<a<12,且对任意t∈[3,5],方程f(x)=g(t)在x∈[3,5]总存在两不相等的实数根,求a的取值范围 .
(a∈R),若0<a<12,且对任意t∈[3,5],方程f(x)=g(t)在x∈[3,5]总存在两不相等的实数根,求a的取值范围 .
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知M为△ABC的中线AD的中点,过点M的直线分别交两边AB、AC于点P、Q,设 ![]() =x
=x ![]() ,
, ![]() ,记y=f(x).
,记y=f(x).
(1)求函数y=f(x)的表达式;
(2)设g(x)=x3+3a2x+2a,x∈[0,1].若对任意x1∈[ ![]() ,1],总存在x2∈[0,1],使得f(x1)=g(x2)成立,求实数a的取值范围.
,1],总存在x2∈[0,1],使得f(x1)=g(x2)成立,求实数a的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知等差数列{an}满足:a3=4,a5+a7=14,{an}的前n项和为Sn .
(1)求an及Sn;
(2)令bn= ![]() (n∈N*),求数列{bn}的前n项和Tn .
(n∈N*),求数列{bn}的前n项和Tn .
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】设点![]() ,动圆
,动圆![]() 经过点
经过点![]() 且和直线
且和直线![]() 相切,记动圆的圆心
相切,记动圆的圆心![]() 的轨迹为曲线
的轨迹为曲线![]() .
.
(1)求曲线![]() 的方程;
的方程;
(2)设曲线![]() 上一点
上一点![]() 的横坐标为
的横坐标为![]() ,过
,过![]() 的直线交
的直线交![]() 于另一点
于另一点![]() ,交
,交![]() 轴于点
轴于点![]() ,过点
,过点![]() 作
作![]() 的垂线交
的垂线交![]() 于另一点
于另一点![]() .若
.若![]() 是
是![]() 的切线,求
的切线,求![]() 的最小值.
的最小值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知圆C:x2+(y﹣1)2=5,直线l:mx﹣y+1﹣m=0.
(1)求证:对m∈R,直线l与圆C总有有两个不同的交点A、B;
(2)求弦AB的中点M的轨迹方程.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com