
【题目】已知椭圆![]() :
:![]() ,四点
,四点![]() ,
,![]() ,
,![]() ,
,![]() 中恰有三点在椭圆
中恰有三点在椭圆![]() 上.
上.
(1)求![]() 的方程;
的方程;
(2)设![]() 的短轴端点分别为
的短轴端点分别为![]() ,
,![]() ,直线
,直线![]() :
:![]() 交
交![]() 于
于![]() ,
,![]() 两点,交
两点,交![]() 轴于
轴于![]() 点,若
点,若![]() ,求实数
,求实数![]() 的值.
的值.
【答案】(1)![]() ;(2)
;(2)![]()
【解析】
(1)根据所给四个点的坐标可知![]() ,
,![]() 关于
关于![]() 轴对称,当恰有三点在椭圆
轴对称,当恰有三点在椭圆![]() 上时,椭圆必经过
上时,椭圆必经过![]() ,
,![]() .将坐标代入椭圆方程可得
.将坐标代入椭圆方程可得![]() 等量关系.由点和椭圆的位置关系,可判断出
等量关系.由点和椭圆的位置关系,可判断出![]() 不在椭圆上,将
不在椭圆上,将![]() 代入椭圆方程,即可求得
代入椭圆方程,即可求得![]() ,得椭圆方程.
,得椭圆方程.
(2)设出直线与椭圆的两个交点坐标和与y轴的交点坐标.利用两点间距离公式可表示出![]()
![]() .将直线方程与椭圆方程联立,根据两个交点可知判别式
.将直线方程与椭圆方程联立,根据两个交点可知判别式![]() ,求得
,求得![]() 的取值范围.结合韦达定理表示出
的取值范围.结合韦达定理表示出![]() .根据坐标表示出
.根据坐标表示出![]() ,再由等量关系
,再由等量关系![]() ,即可消去
,即可消去![]() 求得
求得![]() 的值.
的值.
(1)由于![]() ,
,![]() 关于
关于![]() 轴对称,当恰有三点在椭圆
轴对称,当恰有三点在椭圆![]() 上时,椭圆必经过
上时,椭圆必经过![]() ,
,![]() .
.
所以![]() .
.
又将![]() 代入椭圆方程可知
代入椭圆方程可知![]() ,所以
,所以![]() 不经过点
不经过点![]() ,
,
则点![]() 在椭圆上,所以代入
在椭圆上,所以代入![]() 可得
可得![]() ,即
,即![]()
因此![]() ,
,
故![]() 的方程为
的方程为![]() .
.
(2)直线![]() :
:![]() .则
.则![]() ,设与
,设与![]() 的两个交点分别为,
的两个交点分别为,![]() ,
,![]() ,
,
则![]() ,
,![]()
由两点间距离公式可知![]() ,
,
![]() .
.
将直线方程与椭圆方程联立 ,化简可得
,化简可得![]() .
.
当![]() 时,即
时,即![]() 时,
时,
![]() .
.
所以![]() .
.
由(1)得![]() ,
,![]() 所以
所以![]() .
.
等式![]() 可化为
可化为![]() .
.
因为![]() ,所以
,所以![]() .
.


科目:高中数学 来源: 题型:
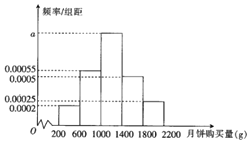
【题目】2018年中秋节到来之际,某超市为了解中秋节期间月饼的销售量,对其所在销售范围内的1000名消费者在中秋节期间的月饼购买量![]() 单位:
单位:![]() 进行了问卷调查,得到如下频率分布直方图:
进行了问卷调查,得到如下频率分布直方图:
![]() 求频率分布直方图中a的值;
求频率分布直方图中a的值;
![]() 以频率作为概率,试求消费者月饼购买量在
以频率作为概率,试求消费者月饼购买量在![]() 的概率;
的概率;
![]() 已知该超市所在销售范围内有20万人,并且该超市每年的销售份额约占该市场总量的
已知该超市所在销售范围内有20万人,并且该超市每年的销售份额约占该市场总量的![]() ,请根据这1000名消费者的人均月饼购买量估计该超市应准备多少吨月饼恰好能满足市场需求
,请根据这1000名消费者的人均月饼购买量估计该超市应准备多少吨月饼恰好能满足市场需求![]() 频率分布直方图中同一组的数据用该组区间的中点值作代表
频率分布直方图中同一组的数据用该组区间的中点值作代表![]() ?
?
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】为了保障全国第四次经济普查顺利进行,国家统计局从东部选择江苏, 从中部选择河北. 湖北,从西部选择宁夏, 从直辖市中选择重庆作为国家综合试点地区,然后再逐级确定普查区域,直到基层的普查小区.在普查过程中首先要进行宣传培训,然后确定对象,最后入户登记. 由于种种情况可能会导致入户登记不够顺利,这为正式普查提供了宝贵的试点经验. 在某普查小区,共有 50 家企事业单位,150 家个体经营户,普查情况如下表所示:
普查对象类别 | 顺利 | 不顺利 | 合计 |
企事业单位 | 40 | 10 | 50 |
个体经营户 | 100 | 50 | 150 |
合计 | 140 | 60 | 200 |
(1)写出选择 5 个国家综合试点地区采用的抽样方法;
(2)根据列联表判断是否有![]() 的把握认为“此普查小区的入户登记是否顺利与普查对象的类别有关”;
的把握认为“此普查小区的入户登记是否顺利与普查对象的类别有关”;
(3)以频率作为概率, 某普查小组从该小区随机选择 1 家企事业单位,3 家个体经营户作为普查对象,入户登记顺利的对象数记为![]() , 写出
, 写出![]() 的分布列,并求
的分布列,并求![]() 的期望值.
的期望值.
附:![]()
| 0.10 | 0.010 | 0.001 |
| 2.706 | 6.635 | 10.88 |
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知圆![]() :
:![]() ,动圆
,动圆![]() 过定点
过定点![]() 且与圆
且与圆![]() 相切,圆心
相切,圆心![]() 的轨迹为曲线
的轨迹为曲线![]() .
.
(1)求![]() 的方程;
的方程;
(2)设斜率为1的直线![]() 交
交![]() 于
于![]() ,
,![]() 两点,交
两点,交![]() 轴于
轴于![]() 点,
点,![]() 轴交
轴交![]() 于
于![]() ,
,![]() 两点,若
两点,若![]() ,求实数
,求实数![]() 的值.
的值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知四棱锥中![]() ,底面
,底面![]() 为菱形,
为菱形,![]() ,
,![]() 平面
平面![]() ,
,![]() 、
、![]() 分别是
分别是![]() 、
、![]() 上的中点,直线
上的中点,直线![]() 与平面
与平面![]() 所成角的正弦值为
所成角的正弦值为![]() ,点
,点![]() 在
在![]() 上移动.
上移动.
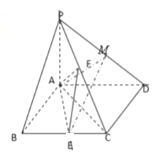
(Ⅰ)证明:无论点![]() 在
在![]() 上如何移动,都有平面
上如何移动,都有平面![]() 平面
平面![]() ;
;
(Ⅱ)求点![]() 恰为
恰为![]() 的中点时,二面角
的中点时,二面角![]() 的余弦值.
的余弦值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】若项数为![]() 的单调增数列
的单调增数列![]() 满足:①
满足:①![]() ;②对任意
;②对任意![]() ,存在
,存在![]()
![]() 使得
使得![]() ;则称数列
;则称数列![]() 具有性质
具有性质![]() .
.
(1)分别判断数列1,3,4,7和1,2,3,5是否具有性质![]() ,并说明理由;
,并说明理由;
(2)若数列![]() 具有性质
具有性质![]() ,且
,且![]() .
.
(i)证明数列![]() 的项数
的项数![]() ;
;
(ii)求数列![]() 中所有项的和的最小值.
中所有项的和的最小值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在平面直角坐标系中,曲线![]() 的方程为
的方程为![]() ,以
,以![]() 为极点,
为极点,![]() 轴的正半轴为极轴建立极坐标系,曲线
轴的正半轴为极轴建立极坐标系,曲线![]() 是圆心在极轴上且经过极点的圆,射线
是圆心在极轴上且经过极点的圆,射线![]() 与曲线
与曲线![]() 交于点
交于点![]() .
.
(1)求曲线![]() 的参数方程,
的参数方程,![]() 的极坐标方程;
的极坐标方程;
(2)若![]() ,
,![]() 是曲线
是曲线![]() 上的两点,求
上的两点,求![]() 的值.
的值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】下列说法中正确的个数是( )
(1)已知沙坪坝明天刮风的概率P(A)=0.5,下雨的概率![]() =0.3,则沙坪坝明天又刮风又下雨的概率
=0.3,则沙坪坝明天又刮风又下雨的概率 ![]() .
.
(2)命题 p :直线ax y 1 0 和3x (a 2) y 3 0 平行; 命题 q : a 3 .则 q 是 p 的必要条件.
(3)![]() 被7 除后所得的余数为5.
被7 除后所得的余数为5.
(4) 已知i 是虚数单位,![]() 复数
复数![]() ,则
,则![]() 最小值是2.
最小值是2.
A.1B.2C.3D.4
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com