
| A. | 3 | B. | 2$\sqrt{2}$ | C. | $\sqrt{10}$ | D. | 2$\sqrt{3}$ |
分析 设点P关于y轴的对称点P′,点P关于直线AB:x+y-4=0的对称点P″,由对称特点可求P′和P″的坐标,在利用入射光线上的点关于反射轴的对称点在反射光线所在的直线上,光线所经过的路程|P′P″|.
解答 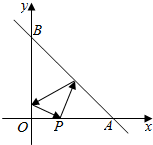 解:点P(1,0)关于y轴的对称点P′坐标是(-1,0),设点P关于直线AB:x+y-2=0的对称点P″(a,b)
解:点P(1,0)关于y轴的对称点P′坐标是(-1,0),设点P关于直线AB:x+y-2=0的对称点P″(a,b)
∴$\left\{\begin{array}{l}{\frac{b-0}{a-1}•(-1)=-1}\\{\frac{a+1}{2}+\frac{b+0}{2}-2=0}\end{array}\right.$,解得$\left\{\begin{array}{l}{a=2}\\{b=1}\end{array}\right.$,
∴光线所经过的路程|P′P″|=$\sqrt{{(2+1)}^{2}{+(1-0)}^{2}}$=$\sqrt{10}$,
故选:C.
点评 本题考查求一个点关于直线的对称点的方法(利用垂直及中点在轴上),入射光线上的点关于反射轴的对称点在反射光线所在的直线上,把光线走过的路程转化为|P′P″|的长度,属于中档题.


科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:填空题

查看答案和解析>>
科目:高中数学 来源: 题型:解答题
 某自来水厂拟建一座平面图为矩形且面积为200m2的二级净水处理池(如图).池的深度一定,池的外围周壁建造单价为400元/m,中间的一条隔壁建造单价为100元/m,池底建造单价为60元/m2,池壁厚度忽略不计.问净水池的长为多少时,可使总造价最低?
某自来水厂拟建一座平面图为矩形且面积为200m2的二级净水处理池(如图).池的深度一定,池的外围周壁建造单价为400元/m,中间的一条隔壁建造单价为100元/m,池底建造单价为60元/m2,池壁厚度忽略不计.问净水池的长为多少时,可使总造价最低?查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 2$\sqrt{3}$ | B. | 2$\sqrt{6}$ | C. | 2$\sqrt{7}$ | D. | 3$\sqrt{3}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | y=x-1 | B. | y=x2 | C. | y=x3 | D. | $y={x^{-\frac{1}{2}}}$ |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com